Many problems in life are harder than the sum of their parts. If you have ever tried to control a group of toddlers you'll know this: two can make good company, three are a crowd and five a riot.
Mathematicians also know that problems can get a lot harder as their size grows. A standard example is the travelling salesman problem, which asks for the shortest route visiting each of a number of cities exactly once. When there are only three cities involved finding the answer is easy, but as the number of cities grows the time it'll take to solve the problem (equivalently the number of steps a computer would have to perform) grows exponentially, so even the fastest supercomputer wouldn't get there within our lifetimes, at least not using the algorithms we know. The travelling salesman problem is a so-called NP hard problem.
One referee said, 'Who would be crazy enough to try to implement this?!' So we had to do it ourselves, and now we've proved our proposal with experimental data. Natalia Berloff
But if ordinary computers can't do the trick, what about quantum computers? Natalia Berloff, Professor of Applied Mathematics at DAMTP, Pavlos Lagoudakis from the University of Southampton, and their colleagues, have proposed and built a quantum device that holds much promise. It's designed to solve a mathematical problem from statistical mechanics that has the same complexity as the travelling salesman problem. The device isn't a full-blown quantum computer because it can't be programmed to solve any problem you like (and doesn't make use of the same quantum phenomena as quantum computers do). It turns out, though, that the problem it is designed to solve has some universality about it. If you can find an efficient method for solving it (one that runs in so-called polynomial time, rather than the much more explosive exponential time) then you can adapt this method to efficiently solve any other NP hard problem.
The problem
Involving both complexity theory and quantum computing, this is a challenging problem to grasp. But to get the gist, imagine a magnetic material, such as iron or nickel. You can think of it as being made up of lots of individual atoms, arranged in an array in space. Each atom has its own tiny magnetic field. The laws of thermodynamics dictate that such a system strives for equilibrium — a state of lowest energy. Since neighbouring atoms can lower their energy by aligning their magnetic fields, they tend to do so. If the temperature of the material is very high, however, thermal fluctuations jostle the atoms and flip their fields, so alignment can't happen. Magnetisation only occurs when the temperature drops below a critical level: large patches of the material then align their atomic fields and the material has become magnetic.
This insight into the workings of magnets gives rise to our mathematical problem. You can represent the array of atoms by an array of points, each of which comes with a variable number called its phase (the direction of the magnetic field) and whose interactions with nearest neighbours are also measured by numbers. You can also write down the formula giving the total energy of the system. This set-up is called an XY model. The task is to find the configuration of phases that minimises the energy. In simple cases this is doable even if the number of atoms is large. In the general setting, however, things can get tricky. Just as the travelling salesman problem, the problem of minimising the energy function of an XY model is NP hard.
Methods for solving XY model minimisation problems do exist but, apart from quickly becoming unfeasible as the number of atoms grows, they come with another potential glitch. They will give you a minimum of the energy function, but this minimum may not be a global minimum. If you think of the energy function as describing a landscape with mountains and valleys, the methods might get you to the bottom of a valley, but this might not be the deepest valley overall. "[The XY minimisation problem] is like looking for a global minimum in a very unstructured terrain," says Berloff. The question is whether a quantum device can do better than classical methods, both in terms of speed and in terms of finding the global minimum.
The solution
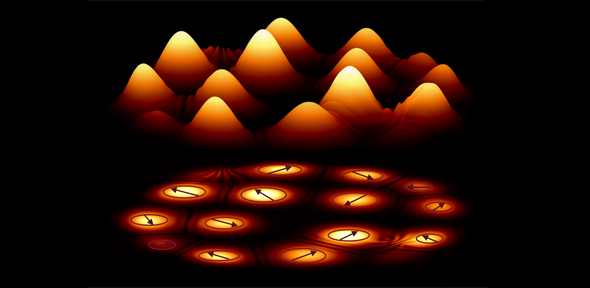
Berloff believes that the new quantum device, which was build at the Skolkovo Institute of Science and Technology, can be more efficient than classical computers and also guarantee to find the global minimum. The device involves quantum particles called polaritons which are half light and half matter (they are in a quantum superposition of both states). Systems of polaritons can be driven to a undergo dramatic change — a phase transition — not unlike the change that happens when a material suddenly becomes magnetised as the magnetic fields of individual atoms align. At the quantum level polaritons, like all quantum particles, can be thought of as tiny oscillating waves. If you increase the density of the polaritons in a system, the tiny oscillators start interacting and synchronise. At this moment the system transitions into a different state of matter, called a Bose-Einstein condensate. Polaritons lend themselves particularly well to this process because they condense at a more reasonable temperature (not too low) and at a lower density than other quantum particles.
In the new device, polaritons are produced at many different sites of a lattice. As the density of polaritons increases, condensation happens, and the researchers can easily observe this. "Before the condensation we see nothing, just noise," says Berloff. "But then 'boom', it condenses and starts to shine light." Each individual condensate comes with a number called the phase (of its wave function). But neighbouring sites also interact through outflowing polaritons. By modifying the distances between sites researchers can finely tune these interactions to mimic the interaction between the atoms in a given XY model. While neighbouring sites influence each other, the system as a whole also naturally chooses a configuration of phases that maximises the number of particles involved. You can write down a formula for the total number of particles — and a few lines of maths show that this is largest when the energy function of the corresponding XY model is at its global minimum. There are several ways in which researchers can read off the final configurations of phases, and this then gives the solution of the XY problem.
The result
So far Berloff and her colleagues have built devices containing up to 100 sites (condensates), but they believe that it can easily be scaled up to thousands of sites. They also believe that for a large enough number of sites, their device will be faster than classical methods.
Does this mean that we will soon be able to solve the infamous NP hard problems with the (polynomial time) efficiency computer scientists deem manageable? Berloff points to an argument, called the NP hard assumption, which decrees that such solutions will never be possible. "[The computer scientist] Scott Aaronson argues that if you could solve NP hard problems efficiently you would become god," she explains. That's because it would enable you to simulate the most complex systems in nature and predict their outcomes. "The NP hard assumption says that such powers will always be beyond human means. We can't escape the assumption, so our [solution time] will still grow exponentially. But the idea is just to do better than classical computing."
Several other mechanisms for solving NP hard problems have been proposed. "We are discussing with other scientists to see who is doing better," says Berloff. "Each platform has its pros and cons, but none has yet become faster than classical computers. So the race is still on."
A major hurdle has been overcome, however. "A few years ago our purely theoretical proposal on how to do this was rejected by three scientific journals," says Berloff. "One referee said, 'Who would be crazy enough to try to implement this?!' So we had to do it ourselves, and now we've proved our proposal with experimental data."
To find out more about quantum computing and complexity classes, read these articles on Plus magazine. You can find out more about the travelling salesman problem in this Plus article.
About the image: Creating polariton condensates in the vertices of an arbitrary graph and reading out the quantum phases that represent the absolute minimum of an XY Model. Credit: Kirill Kalinin.
