In December 2023 the Centre for Mathematical Sciences hosted a celebration of the famous 'hat' tile. The occasion brought together discoverer David Smith, Joseph Myers, the Cambridge alumnus who provided the crucial proof, and Chaim Goodman-Strauss from MoMath in New York to talk more about the fascinating aperiodic monotile.
In March 2023 the world of maths was thrilled by an announcement that even made it into the mainstream news. David Smith - a mathematical hobbyist - had discovered a shape that had eluded mathematicians for some time: an aperiodic monotile, also known as the hat or an einstein.
Just before Christmas David Smith visited the Centre for Mathematical Sciences (CMS) together with two of the mathematicians who helped put the discovery into context: Joseph Myers, Trinity alumnus and former research student in the Department of Pure Mathematics and Mathematical Statistics (DPMMS), and Chaim Goodman-Strauss, outreach mathematician at the National Museum of Mathematics (MoMath) in New York. The occasion was a talk by Goodman-Strauss, organised by the UKMT, with Smith and Myers on hand for questions. The talk introduced the hat and showcased some astonishingly creative ways in which people have made it their own.

The hat is an aperiodic monotile, also known as an einstein.
Tiling the plane
To understand the hat, start by thinking about bathroom walls. They are usually tiled with square tiles. In theory you could continue such a tiling in all directions indefinitely - you could tile the entire two-dimensional plane using squares. Such a tiling is periodic. If you were to pick the whole thing up, move it to the left or right by the width of a tile, and then put it down again, the pattern you'd see would look exactly the same as what you saw to start with. You can make periodic tilings with other shapes too - triangles or regular hexagons, for example. You can also make a periodic tiling using several different shapes.
The question that interested mathematicians was whether you could find a single shape that can tile the plane and for which the pattern you see is not periodic. It's relatively easy to produce such a non-repeating pattern by introducing a small defect in an otherwise periodic tiling, but that feels like cheating. To exclude this possibility, an aperiodic tiling is defined as one that doesn't contain arbitrarily large periodic patches.
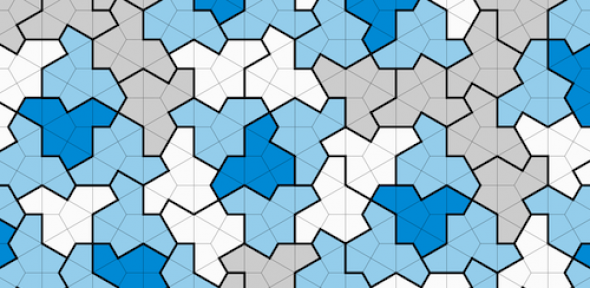
An aperiodic monotile is a single tile that can form an aperiodic tiling of the entire plane. It's such a tile that David Smith discovered. The tile is called 'the hat' because it looks a bit like one (though if you turn it around it looks like a T-shirt). The reason it's also called an einstein is nothing to do with Albert, but with the fact that 'ein Stein' is German for 'one stone'.
A patch of an aperiodic tiling by hats. Image by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, CC BY 4.0 Deed
People have been thinking about aperiodic tilings for a long time. Relevant ideas appear in the work of the 16th century artist Albrecht Dürer and the 17th century polymath Johannes Kepler. In the 1970s the eminent mathematician Sir Roger Penrose built on Kepler's ideas to discover aperiodic tilings that involve more than one shape. Penrose's tilings weren't the first aperiodic ones to ever be discovered (you can see a brief history on Wikipedia), but before the hat came along they were certainly the most famous, and adorn buildings around the world, including the Oxford Mathematics department.
Smith's discovery of a single shape that can tile the plane aperiodically is considered a breakthrough. It's also not just of interest to people who enjoy forming patterns. Aperiodic tilings can be used to understand quasicrystals, types of crystals that were discovered in 1982 by Dan Shechtman and earned him the 2011 Nobel prize in Chemistry (find out more here).
Caught in the wild
There are mathematicians who devote a large part of their time to investigating tilings. One of them is Craig Kaplan, Associate Professor in Computer Science at the University of Waterloo. Kaplan, like most other people working in the field, uses computers to investigate tilings, which makes things a lot easier than cutting shapes out of cardboard.
Hat discoverer David Smith, however, is not a professional mathematician and doesn't normally use computers to play around with tiles. Instead, he uses machine-cut tiles made out of card. Having thought of the hat and seen interesting patterns emerge when putting copies of it together, Smith contacted Kaplan to see if software could produce larger patches of tiling than Smith was able to create manually. Kaplan soon "caught hat fever" and experimented with hat tilings using computation and digital drawings. Within a few weeks he was convinced the hat could indeed tile the plane aperiodically — that it was an einstein. (See this interesting interview with Kaplan by Tim Chartier for more information.)
What was needed next was a proof. To provide the necessary "mathematical muscle", Kaplan and Smith contacted Chaim Goodman-Strauss, who'd been working on tilings for decades. "I immediately suggested they bring in Joseph Myers," Goodman-Strauss told us after his talk at the CMS. "I was sceptical about [the hat] at first, but Joseph was our secret weapon. Normally [proofs] like this might take months, but within about a week of being contacted Joseph produced the first of two proofs [of the hat being an einstein]." (You can see the relevant paper by Smith, Myers, Kaplan, and Goodman-Strauss here.)
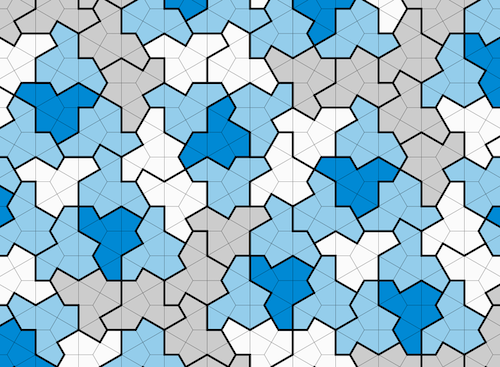
If you have sharp eyes, you might have noticed that in the tiling of hats shown above the mirror image of the hat is used every now and again. Mathematicians tend not to worry about this too much, since the operation of turning the hat into a mirror hat is a simple reflection. Some people have suggested, however, that the need for a mirror hat means that the hat can't be considered an einstein. This might feel a little anticlimactic, but it has a happy ending. A couple of months after announcing the discovery of the hat, the team found another tile, actually a whole family of tiles, called spectres, each of which can single-handedly tile the plane aperiodically without need for mirror images.
What Smith did, says Goodman-Strauss, is akin to catching a never-before-seen animal in the wild. When mathematicians search for tiles with particular properties, they carefully design them, just as you might purposefully breed an animal with the characteristics you'd like. Smith, however, went out looking in the field. He knew roughly where he might find the fabled beast, but the fact that it was actually there couldn't have been predicted.
And this is where the joy of recreational mathematics had a crucial part to play. Had Smith been a professional mathematician, says Goodman-Strauss, he might not have found the hat. "It would have been very foolish for someone who needs to [fulfil professional duties] to even tackle a problem like this, much less to spend the time doing what Dave did, which was to methodically investigate example after example. The structural forces of academia would have made this very difficult."
A life of its own
Tilings have an aesthetic appeal, as well as a mathematical one. One person who has taken the latest discoveries as artistic inspiration is the Faculty's very own David Spiegelhalter, Emeritus Professor of Statistics. "These shapes are a great discovery, all the more extraordinary coming from David Smith working at home," says Spiegelhalter. "I had the huge honour of meeting him this summer in his hometown of Bridlington, Yorkshire, and was inspired to try and make a spectre tiling in stained glass." The result was displayed at Goodman-Strauss' talk to be admired by the audience.
David Spiegelhater's stained glass version of a spectre tiling. "I can't cut sharp concave angles, and so had to break the spectre shape into convex components, but fortunately I could copy a wonderful decomposition into a triangle and five identical 'cairo' pentagons," he says.
The reason Smith, Myers and Goodman-Strauss found themselves together in one place was directly related to artistic interpretations of their work. The day before their visit to the CMS they had been to the House of Commons for the award ceremony of a very special competition. The Einstein Mad Hat Awards were launched jointly by the UK Mathematics Trust (UKMT) and MoMath in September 2023, enabled by support from XTX Markets. The aim of the competition was to find the most creative use people could think of for the hat.
"What was so moving and significant to me was that people made this their own," says Goodman-Strauss. "They took on the hat as something they owned and that they will pass on and share with other people. It's absolutely unique, in my experience, for a mathematical result to have a cultural life like that."
This story is adapted from an article on our Plus outreach website, which also includes more detail about aperiodic tiling and the hat tile. You can find all the winners and honourable mentions of the Einstein Mad Hat Awards competition on the MoMath website.
