
Caucher Birkar, Professor of Mathematics in the Department of Pure Mathematics and Mathematical Statistics, has been awarded a Fields Medal at the International Congress of Mathematicians in Rio de Janeiro. Birkar has been awarded the highest honour in mathematics for his contributions to algebraic geometry.
Exploring algebraic geometry
This area of mathematics does exactly what its name suggests: it tries to understand geometric objects using equations that describe them. It's an idea you might be familiar with from school. For example, the equation
$$y=2x+1$$ describes a line of slope $2$ which intersects the vertical axis of a standard Cartesian coordinate system at the point $(0,1)$. Similarly, the equation $$x^2+y^2=1$$ describes a circle of radius 1 around the point $(0,0)$ in our coordinate system. (This follows from Pythagoras' theorem, see the figure below).
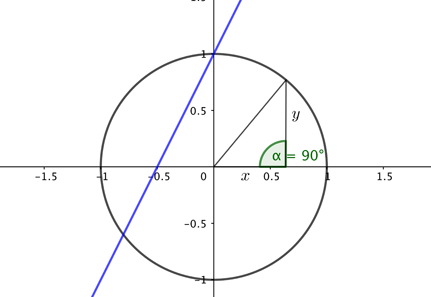
The circle and the line are both examples of algebraic curves in the Euclidean plane: curves that are defined by algebraic equations. Going up a dimension, we can also consider algebraic surfaces. The sphere in 3D Euclidean space that is centred on the point $(0,0,0)$ and has radius $1$ is an example. In analogy with the circle in the dimension below, it's given by the algebraic equation $$x^2+y^2+z^2=1.$$ As you might already expect, a plane in 3D space is another example of an algebraic surface.
But we don't need to stop here: more complicated polynomial equations, perhaps defined over a wider class of numbers called complex numbers, give rise to the general notion of an algebraic variety. Algebraic curves and surfaces are examples of algebraic varieties, but in general algebraic varieties can be much more complex: they can even exist in higher dimensions which can't be visualised. That's not something that deters mathematicians, however, because they've long developed a way of doing geometry even when there are too many dimensions to imagine.
Classifying the infinite zoo
Given the infinite zoo of algebraic varieties that exists, a good idea is to try and classify them into families, just as one would classify a collection of butterflies. Going back to our simple example above, you might want to classify them according to the type of their shapes: things that are like planes go into one family, things that are sphere-like go into another, and so on.
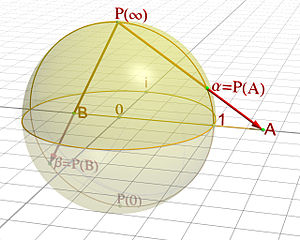
The stereographic projection relates each point of a sphere (apart from the one right at the top) to a point on its equatorial plane: for each point p on the sphere (apart from the one at the top) draw the line that connects it to the point right at the top. That line will intersect the equatorial plane at some point q. Image: Jean-Christophe Benoist.
But you might also allow yourself a little more flexibility. The projection shown in the figure shows how a sphere minus a point can be turned into a plane: essentially, you remove one point, then press the rest of the sphere flat and stretch it infinitely in all directions. It seems that the plane and the sphere are distantly related after all, and we might keep this in mind when classifying algebraic surfaces into families.
The projection we've just considered is an example of a birational map. Birational maps are defined in a much wider context and can be used to link up more complicated algebraic varieties than just spheres and planes. And there are good reasons for why we might link them up in this way. One is that not all algebraic varieties are as nice and smooth as the planes and spheres we thought about above. Some have singular points; loosely speaking pointy cusps. At least when you are dealing with algebraic varieties of a certain type (technically over a field of characteristic 0), the flexibility of birational maps allows you to link such a singular variety to a smooth projective variety without any singular points. Being able to "resolve" varieties in this way is a very useful tool, so there really is some sense in considering varieties that are birationally related as being part of the same family.
Birkar works in the area of birational geometry which is all about classifying algebraic varieties in this way. In particular, mathematicians hope to show that every (projective) algebraic variety is birationally related to a particularly nice kind of variety that is made up of three basic building blocks. For the simplest types of varieties (of complex dimension one) this was already shown by the mathematician Bernhard Riemann at the end of the nineteenth century. Dimension two was sorted out the beginning of the twentieth century. Dimension three only followed suit along time later, between the 1970s and the 1990s. Dimensions four or greater still pose major problems, however, and it's in this area that Birkar has made major contributions. The aim is to show that something called the minimal model programme, an algorithm designed to transfer a variety into one of the three nice building blocks mentioned above, really does work.
A long journey
Birkar was born in 1978 to farmers in the Kurdistan Province of Iran, and went to school during the turmoils of the war between Iran and Iraq. "My city is right on the border. You can imagine we were an easy target. The threat was always everywhere," he told an audience at the International Congress of Mathematicians. "When I was born in my village life was traditional – we produced everything we needed." Explaining how he became one of the world's greatest mathematicians he said, "It has to do with the way of life of the region. The other reason is that Kurdish culture has been conditioned for difficulties by its history. [Also], when I was 10,11,12 my brother helped me a lot to learn mathematics. Family helps enormously – directing, not pushing."
The award of the Fields medal in Rio also made headlines for a non-mathematical reason: as Birkar stood after the ceremony to receive congratulations, his briefcase containing the medal was stolen from directly behind him. The organisers of the conference, and the International Mathematics Union which awards the Fields Medals, went to great lengths to help local police find the thief, and of course, to replace Birkar's medal. The replacement was awarded in a brief but moving ceremony a few days later.
Birkar took the theft in his stride. "This has been widely covered in the media, and now I am more famous than I would have been," he joked as he received his medal for the second time. "And the number of people who know what a Fields Medal is is way more than it was last week."
"In the beginning it was a shock, it happened so fast. But very soon I recovered. In the grand scheme of things this is a really really small thing. I have seen much worse things in my life, and if I was discouraged by such small things I wouldn't be here in the first place."
You can watch our video interview with Birkar here.
Caucher Birkar from simonsfoundation.org on Vimeo.
