
The University of Cambridge is a great place to do a PhD in mathematics. A world class institution, the University received a gold award from the Teaching Excellence Framework earlier this year and in 2014 over 90% of the Mathematics Faculty's staff were classed as world-leading or internationally excellent. But what is it really like to tread in the footsteps of mathematicians like Isaac Newton and Stephen Hawking? And what future lies in store for those who have completed a PhD here?
I love working with other people, I think that's the best thing about being a mathematician. Having people to work with is the most important thing and obviously here at Cambridge there are good people in all areas. Ellen Powell
A good person to ask is Ellen Powell. She has just completed her PhD under the supervision of Nathanaël Berestycki, Professor of Probability at the Statistics Laboratory, part of the Department of Pure Mathematics and Mathematical Statistics.
Meeting the challenge
The word "challenge" comes up a lot when Powell talks about her degree, and for good reason. With the aim of producing some of the best mathematicians in the world, standards at Cambridge are famously high. But for those passionate about mathematics and suited for it, the challenge results, not only in a solid grounding in their field, but also a huge amount of satisfaction. This is something Powell already experienced during her undergraduate degree, which she also took at Cambridge. "[Being an undergraduate at Cambridge] was a different experience to anything I had had before," she says. "I certainly was intimidated at first, but the mathematics was amazing. At school we learnt methods for answering exam questions, and we never really learnt very deeply. At Cambridge you learn from the basics and get a rigorous grounding in maths. It's just a different subject from what it is at school."
The undergraduate mathematics course at Cambridge, called the Mathematical Tripos, dates back to the time of Newton, whose pioneering work in mathematics and physics was a strong influence for many years. It is widely recognised as not only the most demanding undergraduate mathematics course available in Britain but also the most rewarding. Students are supported to meet the challenge, not only by lecturers many of whom are leaders in their field, but also through frequent supervisions in small groups. The aim is to produce the high calibre graduates in mathematics sought by universities and employers in other fields.
In Powell's case the grounding she gained as an undergraduate led on to further study for a PhD. She completed her research degree as part of the unique CCA PhD programme, which emphasises the interconnections between techniques in mathematical analysis and other areas of science, engineering and industry, and their wide range of applications. During their first year students start work on an initial research project, but also work in teams to learn a broad spectrum of modern analysis, and undertake an external project supervised by a user of mathematics in science or industry. And there's another advantage of being part of such a cohort-based programme: the support of other students who go through the PhD experience at the same time and in the same place. "In my case the programme took in about ten people," says Powell. "We all have different supervisors, but were taken through the PhD as group. It also has a social aspect to it. We go out for dinner, or meet up for tea and cake."
Random geometry
With the CCA programme's cross-disciplinary emphasis, it may seem surprising that Powell's research is in an area of pure mathematics. It straddles two areas that at first seem unconnected: probability theory and geometry. But nature provides examples of overlaps and therefore also applications. The motion of a dust particle floating in the air describes a geometrical object — a path in 3D space — and is essentially random, caused by the millions of collisions between the dust particle and air molecules. It's an example of Brownian motion. But although the path is random, and will be different for every single particle that has ever floated around the Universe, probability theory provides ways of describing it. For example, it's possible to work out the probability that the particle has moved a certain distance in any given direction after a certain time (the probabilities follow the well-known bell curve of the normal distribution) and to estimate how often the path returns to a given neighbourhood as time progresses. Albert Einstein was one of first the people to produce a quantitative theory of Brownian motion in 1905. His work helped confirm the kinetic theory of gasses, and provided proof that atoms and molecules, previously hypothetical entities, really do exist.
Today, over a century later, probability theorists like Powell continue to study random curves and surfaces. As an example of something related to her own work Powell quotes models from statistical physics that describe, for example, magnets. These envision a magnet as made up of a collection of electrons which come with a physical property called spin, which can be positive or negative. "You might want to look at interfaces [between clusters of electrons with] positive or negative spins," says Powell. These interfaces form curves or surfaces which, since the behaviour of many particles is involved, are random. "You want to look at what happens to these interfaces as the number of particles in the model goes to infinity. In particular, to see at which scales they still exhibit randomness," explains Powell. "Often the macroscopic randomness is governed by something universal, in the sense that you can take many different physical models, and they will all yield similar behaviour in the limit". Just as you can describe the fluctuations you can expect in the results of an opinion poll that involves sufficiently many people (which are again governed by the ubiquitous normal distribution) so you can describe the fluctuations in random surfaces, as long as sufficiently many particles are involved. The mathematics that is involved in this physically-inspired theory is so sophisticated that the area has become a part of pure mathematics.
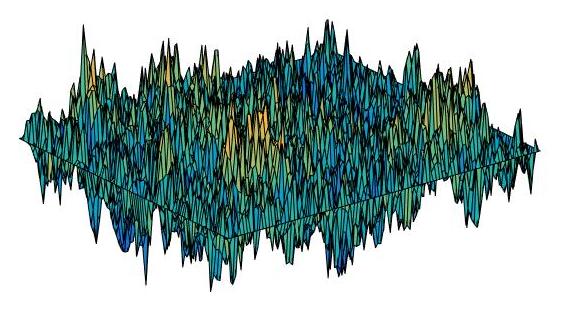
A simulation of a Gaussian free field, an example of a random surface describing the fluctuations of many physical models.
People and travel
Working on such advanced and highly specialised mathematics is again a challenge. "It's a question of finding confidence," says Powell. "And then things start to snowball. When you have your first paper you think, 'right, now I have done something'. After that everything becomes a lot easier. For example, you get collaborators — I love working with other people, I think that's the best thing about being a mathematician. I had a fantastic supervisor here at Cambridge and a great research group with a really nice atmosphere. Having people to work with is the most important thing and obviously here at Cambridge there are good people in all areas."
PhD programmes at Cambridge also place a strong emphasis on travel, which offers students the opportunity to forge connections with leading researchers from around the world. "Within my specific research community there is also a great atmosphere," says Powell. "Because of the emphasis given to travel you meet the same people again and again. We all know each other pretty well now."
For Powell the hard work and benefits provided by her programme have paid off. She has already authored four scientific papers and has decided to stay on in academia. She is set to take up a postdoctoral position at the prestigious ETH in Switzerland in September.
Women in Mathematics
Life as a PhD student is not all about work, of course, so what else do students get up to? Powell decided to take up the cause of women in mathematics. In 21014/15 she was president of the Emmy Noether Society. Run by students at the Mathematics Faculty, the society aims to promote women in mathematics. "The main thing we do is run talks by female mathematicians from all around the world," says Powell. "But we also do social events, like tea and cake, or meetings with female students from other universities."
The aim of the society is to offer female students the opportunity to meet successful role models and to create opportunities for female mathematicians from Cambridge to come together. "One problem that women have in mathematics, and I have experienced that myself, is lack of confidence," says Powell. "But if you see women succeeding in maths, then it's easier to think 'yes I can do that, that's a possibility for me'. It's important that female students know that there are lots of women doing really good maths."
In April 2014 the Faculty's work to encourage and address gender equality was recognised by a Bronze Athena SWAN Department Award. Powell served as student representative on the Athena SWAN committee, contributing ideas to the Faculty's wide-ranging action plan to ensure equal opportunities for women in mathematics. Encouraging girls to take Further Maths at A level is particularly important, says Powell, and outreach activities such as the Faculty's Millennium Mathematics Project are working hard to achieve this.
In summary Powell is happy with her time at Cambridge and proud of her achievements. More importantly, she has found a career path that suits her perfectly. "I love my lifestyle," she says. "You get up and decide what you are interested in thinking about today. If it's good, you can keep working for ages and it's really exciting. If not, then you just think about something else. I never really feel like I'm working."
