
Professor Po-Ling Loh and Dr Varun Jog each bring together different fields in their individual research. Their recent move to the Department of Pure Mathematics and Mathematical Statistics has finally also allowed them to bring together their careers, allowing the couple an ideal setting to further their work.
Varun Jog
Jog was always drawn to mathematics, but engineering schools provided the best education in Mumbai, India, so he did his first degree in engineering. He was naturally attracted to the more mathematical branch of electrical engineering during his studies and got hooked onto information theory during an internship in his third year. Information theory started in 1948 as a means for studying communication, providing a mathematical theory for how much information can be transmitted via various media. "I realised information theory was a sub branch of mathematics. There's unsolved conjectures that inspire you to develop some new maths to solve them. And all of that was very exciting for me."
Over the last decades information theory has evolved to a set of tools that is used in statistics, economics and even finance and gambling. After his PhD in information theory Jog realised he could use these tools in machine learning – the area studying how a machine can learn a task directly from the experience of repeatedly doing that task itself, rather than relying on explicit instructions (in the sense of a traditional computer algorithm).
"We intuitively understand what learning means," says Jog. "But in machine learning we are trying to rigorously define what these concepts mean: when is it possible for an algorithm to learn, how much data are needed for it to learn, and what algorithms are most efficient? There is a lot of scope for using the tools [from information theory] in machine learning. You can get different insights and novel results if you look at it from that direction."
Po-Ling Loh
Meanwhile, Loh had done her PhD in the very new field of high-dimensional statistics. In the last 15 to 20 years fields such as genomics have produced data sets that are very different to those traditionally analysed in statistics. "If you sequence a genome then there are tens of thousands of genes that you are interested in, but the number of people you are sampling is only in the hundreds," says Loh. "When you have these two dimensions playing off against each other – the number of parameters [you are measuring] and the number of samples – you need to do some more careful analysis to understand what is going on."
For her PhD Loh specialised in non-convex optimisation for high-dimensional statistics. Optimisation involves trying to find the minimum (or maximum) of a function, something that is straightforward for convex functions. "The functions that were arising from the types of problems that I was interested in were not convex. Instead of being a bowl-shape [like a convex function] they might have local minima – where a flat place [in the function] might not actually mean that it's the very lowest point."
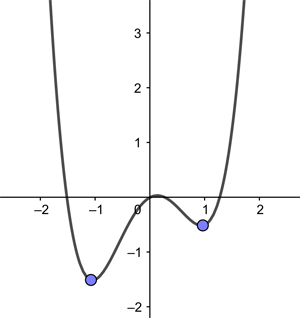
The convex function given by the equation y=x4-2x2+0.5x, has two local minima, one of which has a lower y-value than the other.
Loh realised non-convex optimisation is also something that arises in an area called robust statistics, which studies data that may have been randomly contaminated. The contamination might have come from some systematic source (say from accidental measurement errors) or the data could have been intentionally contaminated by an adversary. This area became popular in the early 1960s and has led to statistical methods that perform well in the face of contaminated data, outliers or with data that doesn't fit an ideal distribution.
"I realised that I've developed all this machinery for non-convex optimisation and high- dimensional statistics, so it would be very easy to plug in some of the notions from robust statistics and prove things about robust estimators," says Loh.
There's been an influx of interest in robust statistics with the development of machine learning. "People knew that these machine learning algorithms were not robust, and the question was how can we make them more robust. That's what I'm currently excited about – studying more robust algorithms and rigorously showing that these methods perform well even when you might be in this high-dimensional statistical setting."
Bringing things together
Until their move to the DPMMS Loh and Jog found themselves dealing with a problem that is common in academia – the two-body problem – where it is difficult for two academics in a couple to both find good positions that are in the same institution, or even in the same city. They'd had to spend a year apart after their PhDs, and in order to find work in the same city again they'd had to make career choices that weren't always ideal.
But moving to DPMMS feels like the ideal move for both of them, as it brings together colleagues from pure maths, statistics and probability in one department. "It feels like the ideal department for both of us," says Jog. "It's a comfortable place and you can easily reach out to different colleagues." He feels that the Department values both his mathematical research into electrical engineering and information theory as important and cutting edge areas of research. "It gives us permission to follow our interests where they lead us. I'm not constrained by the expectations of engineering, there is more freedom to explore the maths that interests [me] that someone else might not follow."
"We're very lucky, it's generally very hard to find two academic positions where both of you feel like you aren't compromising. That's rare," says Loh. "The job at Cambridge is wonderful, we would have both chosen it independently." But thankfully, they could both take up these ideal positions and continue their exciting research careers together.
