
Contents
| News from CMS |
 Aerial shot of the site in July 2002. (pilot: Barry Uscinski; photograph: Louise Hall) |
| Applied Mathematics and the Imaging of the Brain Prof Thanasis Fokas, Department of Applied Mathematics and Theoretical Physics |
Imaging of the human brain provides an example of the enormous usefulness of applied mathematics, and illustrates how the development of new mathematical methods can result in significant technological advances.
Before brain imaging techniques were developed, neurophysiologists gathered information by poking electrodes into the brains of laboratory animals or into human brains during neurosurgery. Neuroscientists were limited to studying patients with damage to specific areas of the brain and looking for links between the symptoms and the site of the damage.
The advent of CT (Computerised Tomography) made direct images of brain tissue possible, and the subsequent development of Magnetic Resonance Imaging (MRI) allowed striking discrimination between grey and white matter. However, CT and MRI are capable of imaging only the brain's structure.
Developments in the late 80s (Functional MRI, SPECT, PET) allowed researchers to begin to study the functional characteristics of the brain. Now it is possible to observe neural activity in living humans noninvasively, with ever-increasing precision. For instance, violin players' atypical dexterity is evident in exceptional representations in the part of their brains which controls the left hand. Using these newer techniques, subtle distinctions can be made. For example, understanding of the context of language is now known to be associated mainly with the left prefrontal part of the brain, while understanding of the emotional tone of speech is associated mainly with the right. Imaging techniques play an important role in the differential diagnosis of schizophrenia and of Alzheimer's disease. They can also be used to study the action of drugs on specific brain receptors, or to see whether genes introduced for gene therapy are working.
What is the value of mathematics in the above imaging techniques? CT is the computer-aided reconstruction of a mathematical function that represents the density of the brain tissue. The line integral of this function is called its Radon transform, and the main mathematical problem associated with CT is how to reconstruct a density function from the knowledge of its Radon transform. The solution to this, the inverse Radon transform, was derived by Radon in 1917. However, in practice the relevant integrals can be measured only for a finite number of lines. Thus the real problem in CT is to reconstruct a density function from a finite number of its line integrals. This problem was solved in the late 60s by A Cormack and G Hounsfield, who were awarded the Nobel prize in medicine for their work. The so-called attenuated Radon transform plays the same role in SPECT (Single Particle Emission Computerised Tomography) that the Radon transform plays in CT. The problem of deriving a formula for the inverse attenuated Radon transform was solved only in 2001 using a new method introduced by the author and R G Novikov. The inversion of the discrete attenuated Radon transform, which will yield better resolution, is work in progress at the Department of Applied Mathematics and Theoretical Physics at Cambridge (DAMTP), in collaboration with a group in France.
Magnetoencephalography (MEG) is another useful imaging technique. Unlike FMRI, SPECT and PET, it has excellent time resolution, although poor spatial resolution at the moment. MEG measures the magnetic field generated by neuron activity in the brain, and attempts to reconstruct the electric current from this measurement. The main difficulty is that the problem of determining the electric current from the magnetic field does not have a unique answer. Although this is well known, the derivation of which part of the current can be determined was obtained only recently by I M Gelfand, Y Kurylev and the author. The numerical implementation of the relevant formula and its generalisation to realistic geometries are currently under investigation at DAMTP using real experimental data from leading brain imaging laboratories in Japan and the USA. The goal is to develop the necessary software so that MEG becomes a major tool for studying brain dynamics.
| Functional MRI images showing the difference in brain activation during a memory test between two groups of subjects. One group carries the apolipoprotein Eε4 allele which is a known risk factor for Alzheimer's disease. This increase in activation may reflect a need to compensate for minor defects in memory - even though both groups appear normal. (Image reproduced with permission from: Bookheimer S Y, Strojwas B S, Cohen M S, et al. 2000. Patterns of Brain Activation in People at Risk for Alzheimer's Disease. New England Journal of Medicine 343 (7), 450-456. Copyright © 2000 Massachusetts Medical Society) | 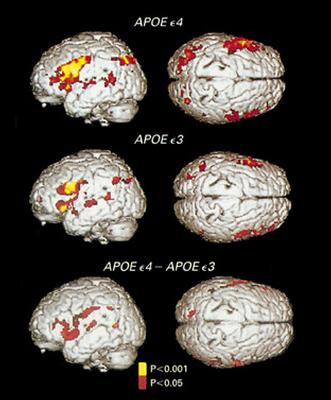 |
| The Art, History and Mathematics of Polyhedra Dr Alan Beardon, Department of Pure Mathematics and Mathematical Sciences |
According to the Oxford English Dictionary a polyhedron is "a solid figure contained by plane faces." Some polyhedra arise naturally as the shapes of crystals. Others are man-made, the earliest examples being the pyramids of Egypt, some of which were built about 5000 years ago. Closer to home, about four hundred small stone polyhedra, dated about 2000 BC, have been found in Scotland. The function of these stones (which can be found in the Edinburgh Museum, and in the Ashmolean Museum, Oxford) is unknown.
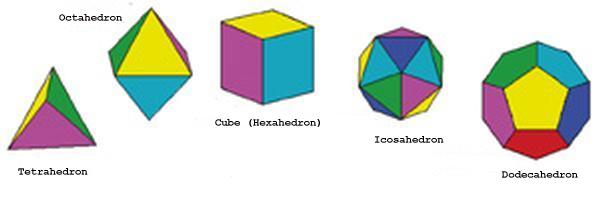 |
The Platonic solids. (Courtesy of Prof Steven I Dutch, University of Wisconsin - Green Bay) |
A polyhedron is said to be regular if its faces are identical regular polygons, and such polyhedra have maximum symmetry. It is a striking fact that there are only five such polyhedra (see above). Plato took these regular polyhedra to represent fire, earth, air, water and the cosmos in an attempt to construct a theory of the universe, and they are now known as the Platonic solids. The first mathematical discussion of polyhedra was given by the Greeks around 400 BC. Archimedes found that, in addition to the Platonic solids, there are thirteen polyhedra in which the pattern of faces around each vertex is identical, and these are now known as theArchimedean solids.
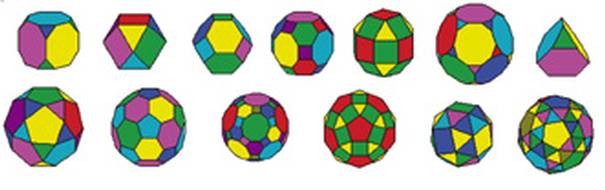 |
Archimedean solids. (Courtesy of Prof Steven I Dutch, University of Wisconsin - Green Bay) |
Plato's ideas survived at least as far as Kepler (1571-1630) who believed that there was a close link between the five Platonic solids and the orbits of the five planets known at that time. During the Renaissance, artists became interested in perspective, and polyhedra offered a challenge to both the artist and the draftsman alike. Leonardo da Vinci drew "skeletal" models of the Platonic solids, and many of his drawings include polyhedra, sometimes as mere "doodles" in the corner of a page. There are some beautiful examples of intarsia (now called marquetry) of this period that include polyhedra. These mosaics have a striking three-dimensional effect which is achieved by using inlaid woods of different colours. Some of the most beautiful of these are by Fra Giovanni da Verona, one of which is illustrated to the right.
 Intarsia panel by Fra Giovanni da Verona in the church of Santa Maria in Organo, Verona. (Courtesy of Kim Williams, photographer) ) Intarsia panel by Fra Giovanni da Verona in the church of Santa Maria in Organo, Verona. (Courtesy of Kim Williams, photographer) ) |
In 1718 Adrian Sharp published a book called Geometry Improv'd in which he showed how to cut a variety of polyhedra from wooden blocks. He calculates all of the measurements to at least fifteen decimal places, although he must have realised (as anyone who has tried knows) that it is difficult even to cut an accurate cube by hand. This book displays a fascination with geometry which goes far beyond carpentry.
Significant advances in the mathematical properties of polyhedra were made by Descartes (1596-1650) and Euler (1707-1783), the most famous of which is Euler's observation that the number of vertices plus the number of faces of a polyhedron is two more than the number of its edges. From this one can deduce that it is impossible to build a polyhedron all of whose faces have, say, six sides. In 1811 Cauchy showed that every convex polyhedron is rigid. A polyhedron is rigid if its shape cannot be deformed without buckling its faces. Whereas triangles are the only rigid polygons (a square, for example, can be "skewed" into a parallelogram), all convex polyhedra are rigid. Cauchy's result raised the question of whether there are any polyhedra that are not rigid, and this was answered by R. Connelly in 1978 when he described a non-convex flexible polyhedron. It is now known that "almost every" polyhedron is rigid. This means that even though we can theoretically "make" a flexible polyhedron, our inability to construct exact angles means that they are, in reality, impossible to construct. In short, the flexible polyhedra are rather like the proverbial "needles in a haystack".
| Tenth Birthday of the Isaac Newton Institute Sir John Kingman, Director of the Isaac Newton Institute |
In July 1992, after years of preparation and building, the Isaac Newton Institute formally opened its doors on Clarkson Road and started its first two programmes. In the decade since it has been the host of 46 programmes across the whole range of mathematics and its applications, from fractals to dynamos, from quantum field theory to Fermat's Last Theorem.
A typical programme lasts for up to six months, and brings mathematicians from all over the world to work together on an area that is in an active state of research. The Institute provides an ideal environment for collaboration, with blackboards throughout its open interior, and an inexhaustible supply of coffee. Participants always praise the helpful staff, who handle the inevitable problems of housing and finance, language and cuisine with enthusiasm and an expertise drawn from long acquaintance with the needs of mathematicians.
| Togliatti's quintic (left) and Barth's sextic (right): surfaces of degrees 5 and 6 with the maximal possible numbers 15 and 65 of isolated singularities. These images were produced as part of the programme entitled "Singularity Theory" which took place at the Newton Institute July - December 2000. (Courtesy of G Gruel) | 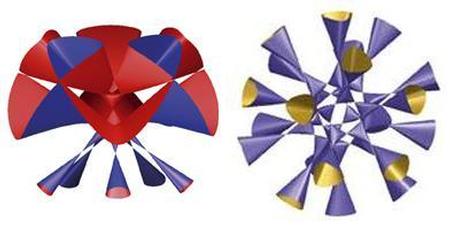 |
Although many of the programmes are purely mathematical in character, some of the most successful have brought together mathematicians interested in a particular, often novel, application, with experts in that application. The Newton Institute environment seems well adapted to getting such people to find a common language, and to break down the barriers that inhibit progress. Areas like financial mathematics, the management of uncertainty, genomics and the spread of epidemics have all been the basis of successful programmes, bringing people from different disciplines together. For example, the epidemics programme brought together statisticians, biologists, medics and sociologists to study the spread of AIDS.
Programmes are selected on the basis of peer review, and where possible decided about three years ahead so that potential participants can fit the meeting in with other commitments. The Scientific Steering Committee, drawn from all over the UK and with members from other European countries, has to look ahead and decide what mathematics will be exciting at that future date. The subject moves so fast that this is no easy task, but the record of timeliness shows that it can be done.
When the Newton Institute opened, it was literally in a green field. Today it is next to the impressive pavilions of the Centre for Mathematical Sciences, and we enjoy the close proximity of the Cambridge mathematicians, pure and applied. Our visitors can not only attend seminars in the two departments, but also enjoy access to the splendid Betty and Gordon Moore Library. But we are a distinct operation, a national research institute serving the whole UK mathematical community. Cambridge undoubtedly benefits from having such a continuing stream of distinguished visitors, but so do the other universities whose staff take part in our programmes, and which can invite our participants to visit their universities too.
 |
Andrei Okounkov in front of the Logan-Shepp-Vershik-Kerov limit shape during the programme on Symmetric Functions and Macdonald Polynomials |
The Isaac Newton Institute now enters its second decade with a high reputation to live up to. We have a pipeline of approved programmes into 2005, in areas such as statistical mechanics of biological systems, Kleinian groups, solar flares and stellar interiors, and applications of mathematical logic. We welcome ideas for new programmes, particularly from those willing and able to take responsibility as future organisers.
For details of coming programmes, workshops and other information, visit http://www.newton.cam.ac.uk.
