Contents
Paul Dirac: predictor of antimatter
Professor Peter Goddard, Master of St John's College, Cambridge
The 8th of August this year sees the centenary of the birth of one of the founders of quantum theory. Paul Dirac was Lucasian Professor of Mathematics in Cambridge from 1932 to 1969 and is numbered alongside Newton, Maxwell, Einstein and Rutherford, as one of the greatest physicists of all time.

Dirac: by permission of the Master and Fellows of St John's College, Cambridge |
Dirac's father, who was Swiss by birth, was the Head of Modern Languages at the Merchant Venturers' School, where Paul Dirac received his secondary education from 1914 to 1918. The young Dirac was required always to converse with his father in French, and he would remain silent unless he could express himself well in the language. This was probably the origin of his legendary taciturnity.
Dirac took his first degree from Bristol University, graduating with First Class honours in electrical engineering at the age of 19, in the midst of the Depression. Unable to get a job, he remained at Bristol and completed the degree course in mathematics as well. Two years later, in 1923, he succeeded in getting a grant to begin research at St John's College, Cambridge. He had hoped to do research in relativity under Ebenezer Cunningham. But, sensing he was near the end of his research career, Cunningham passed Dirac on to R.H. Fowler. Instead of beginning research on geometrical aspects of relativity, Dirac was introduced by Fowler to atomic physics. Very quickly he was plunged into the most profound problems of atomic physics, which was then in an incomplete and paradoxical state.
On 28 July 1925 Dirac attended a seminar by Werner Heisenberg of Göttingen, who at the end of his talk described some new ideas of his, which later turned out to be the origins of his formulation of quantum mechanics. Fowler, appreciating the potential importance of Heisenberg's remarks, encouraged Dirac to try to understand them.
Heisenberg's approach had been to build up a theory entirely in terms of observable quantities, and the observable quantities in atomic theory were mostly concerned with two states of an atom. In this way, Heisenberg was led to associate two-dimensional arrays with observable quantities, and to develop an algebra of such arrays based on physical motivation, without realising that he was re-inventing the algebra of matrices already known to pure mathematicians. The most striking feature of this algebra is that it is non-commutative, that is u times v is not equal to v times u. Out walking on the Gog Magog hills one Sunday in October 1925, Dirac was thinking about the non-commutativity in Heisenberg's algebra, the difference uv - vu, when he suddenly realised the connection between this and a quantity in classical mechanics called the Poisson bracket. Excited, but unable to decide whether there was anything in the idea, he hurried back to his lodgings. His notes and textbooks contained nothing on Poisson brackets and, being Sunday, the libraries were shut. He spent an anxious night waiting, but with his confidence gradually growing, until the libraries opened and he was able to verify that the analogy was perfect.
In the resulting paper, Dirac solved the central problems of atomic theory which had been baffling theoretical physicists for the previous decade. He said in later years that nothing had ever given him as much satisfaction as this first major discovery.
Then a paper by Erwin Schrödinger appeared giving an apparently completely different version of quantum mechanics, "wave mechanics", couched in mathematics more familiar to many physicists. At first Dirac's reaction was hostile but by August he had mastered Schrödinger's formalism and, in arguably his greatest paper, he established the general mathematical framework in which quantum mechanics is now formulated. Within this framework, the distinctions between the Heisenberg and Schrödinger approaches disappear; they are just different choices of systems of coordinates.
Next Dirac applied his general formalism to the electromagnetic field, showing it to be described in quantum-mechanical terms by an assembly of particles (photons), just as had been conjectured by Planck and Einstein in the work which had motivated much of the development of quantum mechanics. In so doing, he brought together the various strands in the development of the subject into a coherent whole, removing once and for all the dichotomy between waves and particles, and simultaneously he created the subject of quantum electrodynamics.
At the end of 1927, the major outstanding problem was how to reconcile quantum mechanics with the other revolutions in physics that had been made at the beginning of the twentieth century, relativity. Many thought that this problem had already been solved but Dirac saw clearly that the supposed solution was unsatisfactory. In 1928, in two papers that are probably his most famous, he produced his relativistic quantum theory of the electron by constructing what came to be known universally as the Dirac equation. It made the previous candidate theory look thoroughly anaemic. Dirac's theory required the electron to have very definite properties (spin and magnetic moment), in agreement with experiment. Moreover, as Dirac pointed out in 1930, it necessitated the existence of another particle with the opposite electric charge and the same mass as the electron. In this way, it predicted the existence of the positron, the anti-particle of the electron, which was confirmed by experiment in 1932. Dirac's prediction of antimatter was described by Heisenberg as "the most decisive discovery in connection with the properties or the nature of elementary particles ... [It] changed our whole outlook on atomic physics completely".
With these developments, quantum mechanics was in an essentially complete form. Dirac's enormous contributions to it were acknowledged by his election to the Royal Society in 1930 and to the Lucasian Professorship in 1932, and by the award of the Nobel Prize for Physics for 1933, which he shared with Schrödinger.
Dirac continued to lecture on quantum theory in Cambridge until his retirement from the Lucasian Chair in 1969. He supervised comparatively few research students, taking the view that the fundamental problems on which he worked were not suited for most students. For many years, his was the first course in quantum theory that a Cambridge student would take. His presentation followed very closely the treatment in his book but, even so, many would attend the course more than once. His delivery conveyed an integrity and coherence of viewpoint that made the line of argument seem inevitable.
If Dirac had done nothing after the early 1930s, he would still be ranked amongst the greatest names in physics, but his work continued unabated in his later years. The first years of his research career were in a golden age in physics, which he played a major part in creating. His later achievements were not on the same scale but neither were those of other physicists. In the following years he worked on a number of topics, writing many papers of great originality. His work on the possible existence of magnetic monopoles contained the seed of the topological ideas that now play a major role in theoretical physics. The significance of this and much of his other work, such as his approach to constraints in classical mechanics, has grown with the years, and his influence is now as great as ever.
His work did not stop on his retirement from the Lucasian Chair. In 1971 he accepted an appointment as Professor of Physics at Florida State University in Tallahassee. There, having Dirac in the Physics department seemed comparable with having Shakespeare in the English department. He continued to work on theoretical physics, until shortly before his death on 20 October 1984.
(Back to top of page)

Professor Michael B Green, Department of Applied Mathematics and Theoretical Physics
In July, DAMTP will host this year's international conference on String Theory at the West Road Concert Hall. This will attract around 400 of the world's leading researchers in an area of theoretical physics that aspires to explain the nature of matter at the tiniest distance scales as well as having important implications for the earliest moments in the evolution of the Universe.
The basic principle of String Theory is surprisingly simple. Whereas in all conventional theories the various fundamental particles are described as point-like objects, in String Theory they are postulated to be tiny strings. The different types of elementary particles - the electron, quarks and many others - appear as different modes of vibration of a single type of string, analogous to the different harmonics of a violin string. This has the potential of unifying all of the observed elementary particles and their forces, including the force of gravity. In addition, String Theory resolves the apparent conflict between quantum theory and general relativity which has beset theoretical physics for the past 75 years.
However, many issues concerning the nature of the theory need to be understood before its physical predictions can be clarified. The simple picture of a string moving through smooth space-time can only be an approximation to a more fundamental principle since in a quantum theory of gravity, space-time itself should emerge as a derived concept, together with the particles and their forces. The search for such an extension of String Theory, sometimes known as "M-Theory", has led to remarkable insights in recent years. This involves connections with supergravity in eleven dimensions, with theories of membranes and their higher-dimensional generalizations, and with the quantum physics of black holes. There has also been a fascinating symbiosis between String Theory and some of the most important areas of modern mathematics.
Strings 2002 should provide a lively forum for leading researchers to present their latest ideas and to conjecture on future prospects for this fast-moving field.
(Back to top of page)
According to folklore a topologist cannot distinguish between a coffee cup and an American donut, as both have one hole. If one imagines both as being made from strong, flexible modelling clay, then either can be continuously deformed into the other without tearing the material. As a topologist I am interested in those properties of geometric objects which, like the single hole above, are preserved under general "non-tearing" deformations.
Seen from an aeroplane it is clear that the surface of the earth is round, although to an observer on the ground it appears to be flat. Locally it resembles the surface of a table. Here the rules of high-school geometry hold, in particular we have the notion of distance between two points. Similarly we can define the distance between two points in 3-dimensional space, which has three independent directions. Objects for which this can be done locally near any point are called "manifolds". The surface of our donut is an example of a 2-dimensional manifold. The solid donut is one of dimension 3; unlike the 2-dimensional surface, it has a boundary. With a little faith one can imagine manifolds with 4 or more independent directions, and so extend these ideas to any number of dimensions.
The main problem for a topologist is how to catalogue manifolds. A set of objects that can be deformed continuously into each other is assigned labels which distinguish it from other sets. These labels are numerical or algebraic and are called invariants, because they do not change when we make a non-tearing transformation. In dimension 2, once it has been agreed that our surface has an upper and a lower side, the only invariant is the number of holes. In dimensions 3 and 4 things are much more complicated and it is not yet clear which labels will specify unambiguously the position of some given manifold in the catalogue. The solution of at least one of the remaining problems offers a large financial reward! In dimensions 5 and higher the situation resembles that of surfaces; the topological class to which a manifold belongs is specified by arithmetic invariants. Formidable computational difficulties remain - enough to keep generations of graduate students busy - but, thanks to the fundamental work done in the 1960s, the way to the classification of high-dimensional manifolds is in principle clear.
As an example consider dimension 6, where the answer is both elegant and of great interest to physicists. In dimension 2, the situation is simplified by restricting attention to surfaces with two sides; an analogous restriction in dimension 6 is to assume that every loop can be shrunk to a point inside the object concerned. Once again the significance of this can be seen from the donut - a loop going round the central hole cannot be shrunk to a point without leaving the donut.
Subject to this "simply-connected" condition and one other assumption, classification up to the most general deformation has been achieved. At least in part the numbers that comprise the arithmetic label, corresponding to the number of holes in a surface, describe how the lower-dimensional sub-objects fit together and turn in on themselves. From the point of view of physics the most recent models for the behaviour of fundamental particles presuppose a small-scale world with 10 dimensions, 3 dimensions of space, 1 of time, and 6 so tightly rolled as to be unnoticeable from the macro point of view. The way in which these extra dimensions have been rolled is described by the labels used by topologists in their abstract classification. The numbers arising for these "Calabi-Yau" manifolds will not be arbitrary, but dictated by physical restraints, and this interplay between arithmetic and physics is of great current interest.
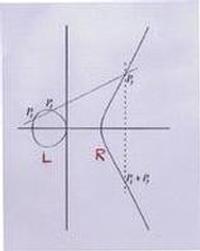
Mathematically the simplest example is given by a hypersurface defined by an equation of degree 5 in 4 (complex) variables. The numbers on its descriptive label show that geometrically it consists of a slightly twisted version of the basic 6-dimensional building block with 102 added handles. As such it generalises the surface of a 102-holed donut. There are lower dimensional analogues of this hypersurface which are illustrated above. In dimension 2 we obtain a cubic curve and in dimension 4 a so-called K3 or quartic surface, both, in contrast to dimension 6, being topologically unique. Inevitably the pictures use real coordinates - introducing i equal to a square root of -1 doubles the dimension in each case. Restricting back to the real numbers halves the dimension; we can visualise this by slicing through our original donut example with a thin metal sheet. The sheet meets the surface of the donut in a pair of circles, corresponding to the two components of the cubic curve (marked L and R in the diagram). Note that component R can be closed by means of an additional, distant, unillustrated "point at infinity". In the same way the two-dimensional surface in the second picture can be thought of as a section through a four-dimensional object.
(Back to top of page)
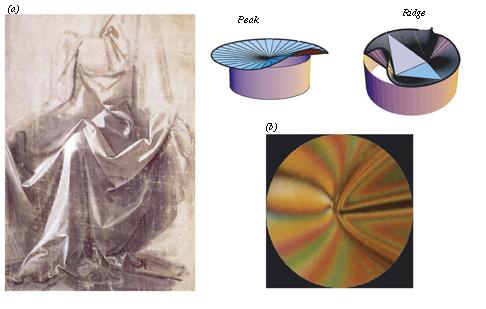
How do you pack a sheet of paper into a sphere much smaller than it? By crumpling it, of course! And why do we care anyway? Because folded, wrinkled and crumpled sheets arise in examples spanning a range of length scales, from the buckled ridges and peaks in a mountain range to the art of fashion draping, and from the wrinkled surface of a raisin to the spiky surface of a diseased red-blood cell. The geometry of the sheet leads to a separation of length scales and immediately biases the class of deformations possible. The constraint of impenetrability leads to a distribution of crumple sizes. The mechanical response of the object determines the ease or difficulty with which the packing may proceed. Thus, these systems offer a rich arena for the interplay between geometry and physics in the mundane world amenable to experience, experiment and theory.
In the drape shown in Figure 1 (a) and (b), we see that the "sheet" is either flat, cylindrical or conical almost everywhere, except along a tenuous network of lines (ridges) which meet at points (peaks), where the deformation is strongly localized. Along these "singular" regions, the surface is doubly curved, and cannot be mapped onto a flat sheet; while away from them, the sheet is simply bent about certain straight lines (generators). Thus, to understand crumpling, we have to ask: (1) What is the geometric and physical nature of the peaks and ridges, i.e. the "singularities"? (2) How do they interact with each other? In Figure 1, we summarize some of our recent results dealing with the shape, response and stability of these "singular" structures and the nature of their interaction in some simple situations. A natural question then arises: Is there a regime where crumpling is analogous to fluid turbulence? (with apologies to Jonathan Swift and Lewis Fry Richardson) as
Big crumples fold into little crumples
That store energy in bending
And little crumples have lesser crumples
And so on to stretching
Analogous situations involving packing arise in the behaviour of fluid filaments and sheets, and are strongly constrained by geometry as shown in Figure 2(a)-(c).
(Back to top of page)