|
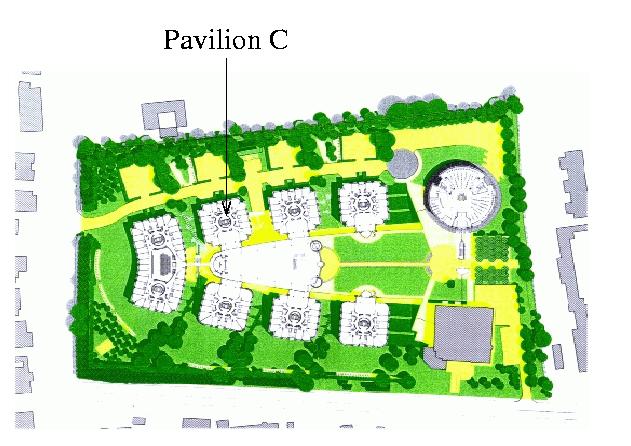
The construction work at the Centre for Mathematical Sciences has now reached an even greater level of excitement and anticipation. Not only are the first pavilions nearing completion, ready for the fit-out phase of the contract, but Pavilion C, the most recent addition to the construction contract has reached the end of its structural frame construction phase well ahead of schedule.
The speed and apparent ease with which the building seems to be emerging reinforces the often heard assertion that all buildings are prototypes. Unlike cars and other products of mass production, buildings are not usually tested to destruction following extensive analysis of models, real and virtual, from which all data is fed back into the reiterative process of design. Not unless the building type is repetitive and required by a professional client, such as a petrol station or warehouse, does the benefit of built models affect the outcome of the design.
However here at the Mathematical Sciences site that process has begun, the contractor having substantially completed the previous pavilions has already climbed the learning curve to a level where the architects drawings are no longer the only guide to the buildings' construction. Techniques and sequences have been altered to optimise the construction programme and avoid previously unforeseen assembly problems.
An obvious example is the lantern which caps the roof structure. Until Pavilion C the contractors construction method was a linear one; following the completion of the roof structure, the lantern was assembled and finished in-situ. This produced assembly and constructional bottlenecks. These are now being negated by constructing the lanterns on the ground, in parallel with the roof construction. The structural design has been amended slightly to suit being hoisted in a substantially complete state into its final position on the finished roof.
The main reason for our excitement over the construction of Pavilion C is due to its ability to complete the northern portion of the Centre for Mathematical Sciences. The whole entry sequence will be in place following its completion; the rhythm of the three Northern Pavilions derived from the scale of the surrounding domestic architecture sets up, as you move past, framed views between them, down their landscaped courts to the Central Pavilion or beyond to more distant landscapes.

These scenographic images should illustrate some of the original intentions of the scheme, an important one being that the development should respond to the surrounding architecture. The neighbouring domestic frontages of the predominantly Thirties and Forties housing, of 32.5m gave us the measure for the rhythm of the perimeter pavilions. The series of pavilions reflecting the scale of the surrounding area then act as a screen to the greater scale of the Central Core, which contains the larger public spaces of lecture rooms and central common rooms, as well as part of the Fluid Dynamics Lab.
The near completeness of the northern portion together with the absence of any southern Pavilions of the Centre, produces an intriguing image of severed incompleteness. I can't help being reminded of Damian Hurst's bisected bovines, or those cut-away jet engines in the science museum. Both bring delight in revealing that which is normally hidden. The omission f the Southern Pavilions allows the larger scale of the Central Core to be revealed and expresses the transitional state of the building.
We architects are fond of this intermediate state, as it reveals the soon to be hidden edifice of a carefully composed building, capable of being enjoyed in the many combinations offered by the realities of the funding campaign. We are however in no doubt as the most pleasing combination of parts, that being the completed pattern of interrelated pavilions set in a harmonious landscape as dipicted on our masterplan.
Progress on Fundraising
E Henderson & S Oliver-Dansie, Development Office |
The phasing of the construction programme for the Centre for Mathematical Sciences is highly dependent on the availability of funds. Since the University receives very little funding for capital investments, philanthropic support for this project is vital. We are therefore delighted to report that so far, £20.25 million has been raised towards the total of £20.50 million for Phase I of the Centre for Mathematical Sciences. This includes donations from former members of the Faculty, from individuals and trusts and foundations, as well as an anonymous donation of £4.06 million which was pledged earlier this year to fund Pavilion 3.
Considerable funding has already been achieved for the Library and Gatehouse, the construction of which is due to begin in February 2000. In October 1998, Dr and Mrs Moore donated £7.5 million for a new Physical Sciences, Technology and Mathematics Library, and in February 1999, Dr Dill Faulkes donated £1 million to fund construction of the Gatehouse, which is assigned to the Newton Institute.
 |
Pavilion B from the east, with the central teaching complex
in the lower left-hand corner |
Construction of Phase I began in May 1998, and the programme is proceeding to schedule and is within budget ensuring that all Cambridge's pure mathematicians can move together into their new home. The completion of the structural construction of the Central Teaching Complex was celebrated on 12th June 1999, at a topping out ceremony, attended by 250 guests and viewed by others on the internet. The remainder of the Phase I funding still has to be found and this is a total of £220,000. A number of initiatives have been undertaken in order to close the gap, and an evening of talks followed by a dinner at Jesus College, kindly sponsored by John Wisbey and Ian Peacock at Lombard Risk Management, was enjoyed by those Friends of Mathematics at Cambridge who have supported us in our endeavours.
A fundraising strategy is under way for Phase II of the project which consists of the final four pavilions. If you would like to find out how you too can become involved in this project which is of vital importance to the development of teaching and research in mathematics at Cambridge, then please contact either Elizabeth Henderson or Sophia Oliver-Dansie at the University of Cambridge Development Office,
10 Trumpington Street, Cambridge, CB2 1QA, tel: 01223 332288.
| Thanks
We should like to thank all those members of the Institute of Actuaries and their friends, who have collectively donated over 100,000 pounds towards the new lecture theatre which will be housed in pavilion D. This is a magnificent achievement which has helped progess plans for the immediate future, and will contribute greatly to the teaching of mathematics into the 21st century. Thank you for your generosity.
|
Applied Pure Mathematics
T W Körner |
Since the time of Pythagoras people have sought, with gradually increasing success, to understand and control nature using mathematics. But mathematicians have also developed their subject as an end in itself. We distinguish between pure and applied mathematics although it is clear that the same impulse drives humanity to try to describe the first minute of the universe as to prove Fermat's last theorem.
That pure mathematics derives many of its problems and methods from applied mathematics is obvious enough. The beautiful edifice of Greek geometry grew out of problems in measuring farmers' fields. My own subject of Fourier analysis grew out of studies of heat conduction and the vibration of strings. But does applied mathematics obtain any benefit from pure mathematics?
It is said that the Amazon rain forests are a major resource for humanity because they contain so many different plants some of which will have presently unknown but vital uses in the future. Pure mathematics represents a similar resource full of species --- some beautiful, some grotesque, all useless at present (or they would already be applied mathematics) but a few which will have remarkable uses in the future.

The Greeks developed the theory of conic sections for its own sake but when Kepler sought the paths of the planets he discovered that those paths were ellipses. In 19th century Cambridge when mathematicians studied the many dimensional generalisation of ellipses to ellipsoids they studied them mainly for their own sake (and as a source of examination questions). However, when Pearson asked how we can test statistical laws, the mathematics he required was precisely that of the ellipsoid.
In the 1860's Cayley, a professor at Cambridge, introduced the notion of a matrix. To the mathematicians of the time this must have appeared simply as a variation on the much older notion of the determinant. Moreover this variation had a deeply unpleasant property. If you multiply two matrices A and B you get two different answers according as you multiply them in the order AB or BA. (Of course, if you put your shoes and socks on you get a different result according as you adopt the order `shoes, socks' or `socks, shoes'.) Eighty years later, when Heisenberg sought to build a new quantum mechanics on the ruins of the old he found that "There was a very disagreeable situation [since in the new theory] xy is not equal to yx... it worried me terribly". He sent his work to Born saying that "he had written a crazy paper and did not dare send it for publication". Born remembered matrices from his student days and realised that the mathematics Heisenberg required already existed.
In the same way when, a few years earlier, Einstein sought a theory of General Relativity he discovered the key in theories of differential geometry developed earlier by Gauss, Riemann and Italian geometers. In turn the new applied theories of relativity and quantum mechanics paid back the pure mathematical fields they used with a stream of beautiful new results and puzzling questions.
Pure mathematical ideas turned out to have useful applications in new fields far from the traditional ones of physics and engineering. Polish mathematicians worked out the internal structure of the Enigma coding machine using group theory and Turing and others used ideas from mathematical logic to build the machines which decoded the U-boat signals and so helped win the Battle of the Atlantic.
Twenty years later, mathematicians had the happy idea that the way to construct a difficult code is in such a way that solving the code is equivalent to solving a difficult problem in pure mathematics. At the moment we can only produce codes whose solution is equivalent to a problem that mathematicians believe to be difficult but even these are so good that the US government classifies them as weapons of war.
Code making and code breaking are romantic and, in these days of the Internet, commercially important. However, the real money lies in the economic and error free transmission of ordinary messages. Here mathematicians have shown that the problem is effectively that of efficiently packing oranges in a crate. Unfortunately, the crates and oranges are 50 or 100 dimensional crates and oranges and all the obvious ways of packing are incredibly wasteful. It can be shown that throwing the oranges in at random is an excellent way of packing but randomly packed crates are hard to unpack. Those seeking good non-random packings use ideas from branches of abstract algebra which fifty years ago would have been considered the purest of pure mathematics.
In my view, if the rain forests are to be preserved it should be because they are marvellous and beautiful and not because they are a possible economic resource. In the same way, pure mathematicians should pursue pure mathematics for its own sake. But we should be pleased when a theory developed for its own sake turns out to be useful.
*****
Dr Tom Körner is Reader in Analysis in the Department of Pure Mathematics and is the author of ``The Pleasures of Counting'' published by the Cambridge University Press. ``A cracking good tale; buy it for your children and read it yourself'' -- Mathematika.
STIMULUS and askNRICH -- PEER ASSISTED LEARNING
T Beardon, University of Cambridge School of Education, Millennium Mathematics Project |
| `We enjoy learning' is the message of STIMULUS and askNRICH, both community service links between Cambridge University and schools whereby university student volunteers, from the Mathematics, Natural Sciences, Medical Sciences, Computer Sciences and Engineering, provide peer assisted learning (or PAL). |
| |
| ``Very interesting to see how children's minds work, the scientific basis we take for granted - conducting experiments and proving results all takes a long time to learn - I'd forgotten that! Children are fun, they treat you differently to the teachers, as more of an older sibling but with the respect and interest in what you are teaching.'' (Lizzie Pomeroy, Trinity College, Girton Glebe Primary School.) |
| ``I went into a comprehensive school much like the one I attended. Year 7 were really keen to learn, or at least most of them were! The staff were grateful for my help as there is no way in which one teacher can provide each child with the individual attention they needed to answer their problems. It felt good to be doing something genuinely useful.'' (Tomos Reed, Emmanuel College, Coleridge Community College.) |

STIMULUS (set up in 1987 by Toni Beardon) and askNRICH (set up in 1997) are projects based in the University School of Education and partners in the Millennium Mathematics Project. Each year about 70 volunteers help in 25 local schools choosing the age range of pupils and either Mathematics, Science, Technology, Information Communication Technology (ICT) or Personal Social and Health Education lessons.
| ``When I arrived each Tuesday the class teacher gave me an outline of what she wanted me to cover with a group of 6 or 7 children. I either worked with the outstanding students or those struggling. I took 5 minutes to brainstorm keywords and ways of illustrating the concepts. Then I held quite an informal class concentrating on the particular needs of my students. There was generally a lot of fun but I usually drove the points home one way or another. I cherish those afternoons.'' (Stephanie Cohen, Robinson College, Girton Glebe Primary School.) |
| ``Being involved in STIMULUS has been very beneficial to me. Not only has it provided an afternoon away from the strains of student life but it has reinforced my desire to work with children after I leave higher education. The staff at the school were not afraid to give me responsibilities and seemed glad that I was there. For the sense of fulfilment it brings I would recommend STIMULUS to anyone whether or not they were considering teaching as a possible career.'' (Paul Thompson, Selwyn College, Queen Edith's Primary School.) |
The askNRICH service answers mathematical questions from thousands of school students and teachers all over the world providing PAL on the Internet via the NRICH website. The NRICH Online Maths Club (http://nrich.maths.org) has over 30,000 regular users in more than 70 countries reading the web magazine, solving NRICH problems, and discussing maths via the askNRICH webboard and email newsgroups.
| ``AskNRICH is brilliant. I can ask all the questions I want. The answers are fascinating because they take you further than you were asking plus you have a decent conversation with someone who knows much more than you about maths.'' (School student, aged 17.) |
Evaluations show a win-win situation with benefits for the university students, teachers and pupils alike. For university students PAL is enjoyable; it provides training and opportunities that they don't get through their courses to develop social, organisational and communication skills. For teachers and pupils it provides valuable support giving many youngsters more individual help and attention than the teacher is able to give alone.
 |
STIMULUS has been generously funded by the Ford Motor Company |
| STOP PRESS
The Trade and Industry Secretary announced on 7 December 1999 a grant from the Joint Infrastructure Fund towards Phase II of the Centre for Mathematical Sciences project.
|
|

