
It may not be a great comfort to know that virtually all structures -- including the aeroplanes in which we all fly -- contain cracks! There is, however, a well-defined subject called fracture mechanics. A crack does no harm so long as it does not grow catastrophically. To explain, it is necessary to talk about stress. This is force divided by area. Its significance may be related to common experience by considering whether you would prefer to have your foot trodden on by a heavy man wearing big shoes, or by a diminutive lady wearing stiletto heels: the former applies the greater force but it is spread over a bigger area and so is less damaging. The paradox with a crack is that very high stresses are unavoidably generated near its edge. The simplest theory actually predicts that these stresses become infinite. Why, therefore, is the material not pulled apart? More refined theory (which involves the analysis of a set of nonlinear partial differential equations) shows why the stresses near the crack edge in fact remain finite. Thus, it explains why the crack need not extend, until the applied loading is sufficiently intense. More important, it shows the precise way in which the simplest theory becomes modified by the nonlinearity, and provides the engineer with an easily-- parameter -- the `stress intensity factor' -- which should not be allowed to exceed a critical value. Even theory at this level suffices for much of engineering design and analysis, and is employed, for instance, in conjunction with programmes of inPservice inspection of airframes and aero engines to decide when a component should be removed from service. Modern materials are often so tough that the assumptions underlying the simple theory do not apply: they withstand much larger stresses and more sophisticated theory is needed. Research is still progressing in some areas but much understanding has already been acquired and is exploited in practice. A problem under active study at present is the dynamic propagation of a crack. The equations describing propagation are exceptionally difficult to solve, but noteworthy progress has recently been made, and the resolution of questions such as why cracks tend to branch when they run fast is in prospect. Different examples of failure are provided by microelectronic components. A silicon chip is often sealed within a plastic block and it is important that this plastic package should remain bonded to the chip. The package is nearly always under stress, introduced upon cooling from its fabrication temperature, so decohesion is a possibility. Such devices are inspected after manufacture, and those with cracks are discarded. The problem here is the development of efficient and economic methods of inspection. Ultrasound is used and the problem is to identify those characteristics of the returned signal that diagnose the state at the chip-package interface. Theory underpinning a novel use (at the National Institute of Standards and Technology, Washington, DC) of an Tacoustic microscopeU, in which amplitude rather than travel time is mapped, is under development in the Department. There are other semiconductor devices in which stress is `designed in', to achieve a desired electronic performance. A thin layer consisting of a mixture of silicon and germanium may be deposited on a substrate of pure silicon, for example. The atoms tend to line up, even though the germanium atoms would prefer more space, so the layer is under stress. Failure in this context means relaxation of the stress by some means: the device remains intact but its performance alters. Mechanisms for stress relaxation (involving the introduction of dislocations), and means for its avoidance, have been clarified through work within the Department. Another development was the first satisfactory explanation of the relation between elastic mismatch and electronic performance of `quantum wire' structures. Almost all of this work is inter-disciplinary in nature: the theory can be done in the Department but it has to address the right problems! Often this involves collaboration with some outside organisation. There are, however, also strong interdepartmental links within Cambridge, and one quite recent development has been the establishment of the Cambridge Centre for Micromechanics, whose participants come mainly from DAMTP, and the Departments of Engineering and Materials Science. Present concerns of the Centre include analysis of the shock-absorbing capacity of metal foams and (avoidance of) the failure by micro-buckling of fibre-reinforced composites. The Centre provides, internally, a forum for collaboration and, externally, a strong interdisciplinary group with the potential to tackle challenging problems in materials technology. |
| The Faulkes Gatehouse By Professor Keith Moffatt, Director of the Isaac Newton Institute for Mathematical Sciences |
|
The Dill Faulkes Educational Trust has made an exceptionally generous donation of one million pounds to the Isaac Newton Institute for Mathematical Sciences, to finance construction of the Gatehouse on the Clarkson Road Site. The Gatehouse is strategically placed at the east end of the site, between the Newton Institute and the new library. It will provide the main access to the site for all pedestrians and cyclists approaching from the Grange Road end of Clarkson Road. It is on the main east-west axis of the site, and is of central importance from an architectural point of view. The Architects have responded to the challenge with a building of exciting design. It contains a semi-circular Seminar Room, accommodating 50, at first floor level, and three `pi-by-three' offices at ground floor level. The building is completed by staircase and lift leading to a landing over the archway entrance to the site.
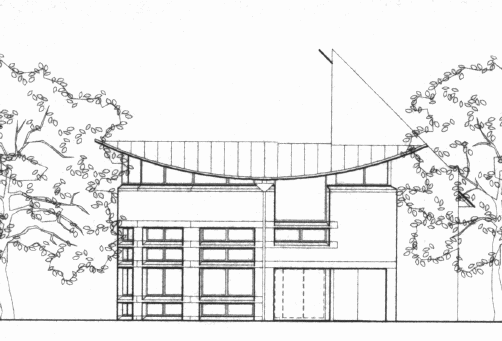 The General Board has agreed to assign the Gatehouse to the Newton Institute, with the proviso that the Seminar Room may, when circumstances permit, occasionally be made available for Departmental use. The Newton Institute is the national institute for the mathematical sciences. It was established in 1992, and was this year awarded one of the prestigious Queen's Anniversary Prizes for Higher and Further Education, in recognition of its achievements over the last seven years. The Institute runs visitor research programmes on selected themes which attract leading specialists world-wide, for periods of up to six months, for intense interactive research. The current programmes are on Complexity and Information Theory, on Structure Formation in the Universe, and on Solid Mechanics and Materials Science. These programmes are all deliberately interdisciplinary in character, and demonstrate the wide applicability of mathematics to a very great range of problems of public interest and concern. |
| Asymptopia |
|
Our newsletter now has a new format and a new name. Mathematicians (including those who progressed no further than `O' levels!) will recall the term asymptote as describing a curve that gets ever closer to a straight line. The point at which they finally meet is asymptopia and we are hoping that the plan for a new home for mathematics in Cambridge is reaching its own Asymptopia.
If you would like to receive notice when the next issue is published, please send your email address to P.V.Landshoff@damtp.cam.ac.uk
|



