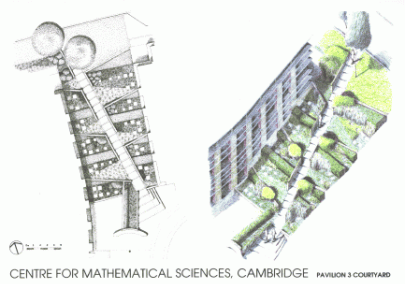
| Common Ground: Landscape Design at the Centre for Mathematical Sciences Livingston Eyre Associates, Landscape Architects |
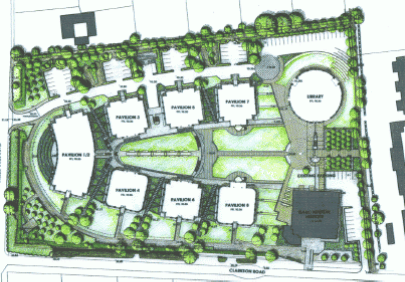
Park. Court. Square. Garden. Four words that conjure up strong images of manmade spaces for most people, and especially so for landscape architects. These spaces have evolved from very disparate original functions and meanings into recognisable components of our modern civic fabric. These kinds of public space, together with the systems of interior rooms that buildings enclose, form a continuum of human interchange. Outdoor rooms and interior landscapes are indeed familiar turns of phrase which serve, on consideration, to emphasise the existence of this undervalued relationship between the inside and the outside world we build for ourselves. It is a reasonably infrequent occurrence for a landscape architectural firm to design a single project - a single building site - that is composed of more than two or three main types of public space. Here at the Centre for Mathematical Sciences is an architectural design, born of a client brief, that sets the stage for an unusually rich matrix of exterior public space. Thomas Jefferson, at the University of Virginia, created a wonderfully subtle and elegant system of spaces - what he termed an "academical village" - which has much resonance with the architectural scheme for the Centre. It was Jefferson's genius at Virginia and it is our charge at the Centre to extend and explore the idea of a community of scholars as an urban paradigm using a kit of parts - park, court, square, garden - that supports the client's needs and affirms shard notions of good public spaces. Park Court Square Garden Planting concept |
| Ozone Holes and the Sun's Interior By Michael McIntyre, Department of Applied Mathematics and Theoretical Physics (DAMTP) http://www.atmos-dynamics.damtp.cam.ac.uk/people/mem |
|
Why, sceptics often ask, do the strongest ozone holes appear in the south, in the stratosphere over Antarctica, when the man-made chlorofluorocarbons (CFCs) said to be causing them are emitted mainly in the north? An adequate answer involves complicated chemistry and radiation - infrared, visible and ultraviolet - and complicated fluid dynamics. To understand what is going on in the stratosphere, we have to deal not only with the chemistry and radiation but also with exotic wavelike and turbulent motions in a strongly stratified, rapidly rotating fluid. Today's understanding of these motions, owing much to research done in DAMTP, tells a remarkable story of order emerging out of chaos. Some of the order can be traced to the strong chirality, or handedness, imposed by the sense of the Earth's rotation. Coriolis effects are crucial here - even though, contrary to what you might read in the newspapers, they are quite unimportant for the water in your bathtub. (I recently read in a very prominent newspaper that Ecuador, being eponymously on the equator, is the country where the bathwater doesn't know which way to turn.) More seriously, there is now an overwhelming weight of evidence (not recognized by all newspapers) that the ozone hole is, indeed, caused mainly by CFCs and other man-made chemicals. What happens is this. CFC molecules go on epic journeys. They wander around the lower atmosphere for times of the order of a century, visiting the southern as well as the northern hemisphere again and again, before entering the stratosphere or dissolving in the ocean. The majority eventually enter the stratosphere, via the tropics. The Coriolis effects make the stratosphere into a gigantic suction pump, inexorably pulling air upwards from the tropical lower atmosphere and pushing it polewards and back downwards in higher latitudes, over tortuous pathways, in some cases all the way to the Arctic or the Antarctic. This is order out of chaos on a grand scale. The journey through the stratosphere takes several years, and, at altitudes above about 25 km, brings the CFC molecules into the glare of hard solar ultraviolet. The photons are energetic enough to break the tight chemical bonds that give the CFCs their stability and non-toxicity at sea level. The broken molecular fragments are very reactive and enter a complicated chain of chemical events. It is they and their reaction products that bring about the destruction of ozone - most conspicuously under the extreme conditions of the Antarctic polar stratosphere, but also, to a lesser extent, in many other places including the Arctic. And what has this to do with the Sun's interior? Our understanding of the stratospheric pumping action, plus the latest observational data, has led to what I think will be a breakthrough in solar physics. Coriolis effects are once again important. The Sun's turbulent convection zone, shown orange in the figure, pumps a circulation in the underlying 'tachocline', shown green with its thickness exaggerated for graphical clarity. Confronting the fluid-dynamical theory with the data, we are forced to a radical conclusion: the Sun not merely can, but must, have in its stably stratified interior a magnetic field (red lines) that is strong enough to reshape the circulation and differential rotation in the interior (see figure caption). This has far-reaching consequences for understanding solar spindown history and possible internal variability, and promises to solve a longstanding puzzle about the destruction not of CFCs but of lithium. It should yield otherwise unobtainable information about the Sun's deepest interior, adding value to the observational data. Space precludes further explanation here, but a first report has already appeared in Nature (20 August 1998), written by Douglas Gough and myself. |
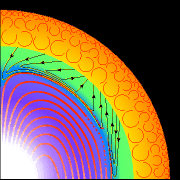 Schematic slice through the Sun. The tachocline (green) has strong shear or differential rotation. It is much thinner than shown, about 2% of the Sun's radius. The circulation pumped by the overlying convection zone (orange) tends to burrow inexorably downward into the Sun's interior, which is stably stratified like the Earth's stratosphere. If nothing else were happening then the tachocline would be too deep, today, for consistency with the data. Something must be stopping the circulation from burrowing downward. The only possibility is an interior magnetic field such as that shown by the red field lines. The circulation skims off magnetic flux like a fruit peeler, gradually feeding it into the convection zone. The dynamics could be chaotic and could have unexpected effects on the seeding of the solar dynamo, with implications for sunspot activity and possibly for climate variability, as in the so called Maunder Minimum of the 'Little Ice Age'. |
| The Millennium Mathematics Project http://www.mmp.maths.org.uk |

From July 1999, Professor John D. Barrow will join DAMTP as a Research Professor of Mathematical Sciences and Director of the Millennium Mathematics Project. This exciting new project aims to improve the understanding and appreciation of mathematics amongst young people and the public at large. Stimulated by the challenge of reversing falling levels of numeracy amongst young people, it will build on the successes of NRICH and PASSMath, our existing web-based programmes for schools, but seek to promote mathematics in new ways and in new places. The challenge of stimulating interest in mathematics amongst school students and maintaining that interest in gifted pupils is one that should be of concern throughout the UK business and industrial communities. The new millennium will present us with a world of growing technical complexity where an ability to appreciate the patterns, programs, risks, and complexities of the world will require familiarity and expertise in mathematics. The Millennium Mathematics Project aims to help ensure that our educators and young people are introduced to the appeal and central importance of mathematics in ways that display its relevance to the commercial, scientific, and cultural worlds. We recognise also that just as there are many who can appreciate and value music or painting without being musicians or painters so we must encourage an appreciation for mathematics and the insights that it can give into the patterns in the world around us. John Barrow is well suited to lead this Project. Besides being known for his work in cosmology and mathematical physics, he is a prolific author and lecturer committed to the public understanding of science. He has written ten books about a wide spectrum of subjects that expound what is happening in science and mathematics and which highlight their connections with other human interests, in art, music, history, and the great questions of existence. Previously, he held positions at the Universities of Oxford, the University of California at Berkeley, and Sussex where he is currently Professor of Astronomy, Director of the Astronomy Centre and PPARC Senior Fellow. He is a frequent contributor to the print and broadcast media in the UK and abroad. He gave the 1989 Gifford Lectures, and many other public presentations to audiences from a wide range of backgrounds. He also has the unique distinction of having delivered invited lectures on mathematics and science at 10 Downing Street, Windsor Castle, and the Vatican Palace. |
| Cambridge Mathematicians win Fields Medals |
|
At the International Congress of Mathematicians in Berlin in August, Cambridge University mathematicians won two out of the four highly prestigious Fields Medals, the highest accolade for mathematics, awarded every four years, and equivalent to the Nobel Prizes. Richard Borcherds, a Royal Society Research Professor, and Tim Gowers, the Rouse Ball Professor of Mathematics, both work in the Department of Pure Mathematics and Mathematical Statistics and completed the Mathematical Tripos and their doctoral studies at Cambridge. Richard Borcherds won his award for initiating a whole new field of study in algebra, called "Vertex Algebras". This new mathematical concept has profound connections with other well-established areas of pure mathematics and with some of the latest developments in theoretical physics. Borcherds' vertex algebras are closely connected with, and were in part motivated by, a theory developed by physicists called string theory. String theory is aimed at providing a unified understanding of all the basic forces and fundamental particles of nature. Borcherds uses theorems from string theory in his work and a new sort of algebra he has introduced, called "generalised Kac-Moody algebras", seems, in turn, to be playing a role in the latest developments in string theory. Tim Gowers' award is for his spectacular applications of new combinatorial methods to solve problems in probabilistic number theory and Banach spaces, invented by Polish mathematician Stefan Banach in the 1920s, which provide a unifying framework for many mathematical results and phenomena. His most recent work, which is said to have captured the enthusiasm of the Fields' committee, involves a new proof of a theorem of a Hungarian mathematician called Endre Szemerédi. This theorem proved a conjecture of Erdös and Turan, two famous mathematicians from Hungary, that a sufficiently dense set of integers must contain arithmetic progressions of all lengths. "It might not sound that interesting to reprove an existing theorem," says Gowers, "but my proof gave far more information and introduced techniques that will almost certainly be useful for many other problems." |