
|
Monday 1 October 2001 saw the successful culmination of several years of planning and preparation as the Betty & Gordon Moore Library opened its doors to readers for the first time.
I first saw the building in late June, when it was still necessary to don a hard hat and blue plastic overshoes before venturing inside. As the tour was part of the interview process for my current r“le as subject specialist for mathematics and physics, this was perhaps not the best time for architectural appreciation. However, the impression then formed of a hugely elegant building has remained with me, and my admiration has only increased with greater appreciation of the skilfulness of its synthesis of functionality and style. The readers generally seem to concur in this view, and the second floor is proving particularly popular as a study area, with its light, airy, and tranquil atmosphere.

The Moore Library's brief, as the newest dependent library of Cambridge University Library, is to support the University's research activities in mathematics, the physical sciences, and technology. In appropriately 21st century fashion, this is achieved using the `hybrid' library approach; that is, by supplying information with relevant content irrespective of its format. Unrivalled access to print material is provided by housing the entirety of both the monographic and periodicals collections on open shelving, while electronic sources are made available via a large cluster of computer workstations.
Although books and computers could be accommodated effectively in some kind of warehouse, such a solution would ignore the needs of readers. In contrast, the real building is carefully designed to provide attractive study and reading areas as well as plenty of storage space.
Back on that opening Monday our first visitor, Professor Grimmett, kindly congratulated and thanked staff for their efforts in readying the Library for readers. Even in my short association with the Library, it has become obvious that this appreciation and gratitude needs also to be expressed to the much wider group of people involved with the project in a vast range of capacities; not least to those whose generosity has made the whole thing possible.
If you have not yet been able to visit, might I suggest that the Library (and, in fact, the whole site) are well worth adding to your itinerary next time you are in Cambridge?
| Avalanches, mud flows, oil spills and volcanic eruptions Professor Herbert E Huppert, Institute of Theoretical Geophysics |
Avalanches, mud flows and gigantic oil spills are all examples of a class of fluid flows called gravity currents. Gravity currents occur whenever fluid of one density flows into a fluid of a different density. Such forms of motion occur, for example, as sea-breeze fronts in the atmosphere, when cold, dense air intrudes under relatively less dense air; in the oceans, when the hot salty effluent of the Mediterranean flows through the Straits of Gibraltar and intrudes into the colder, less salty Atlantic at a depth of approximately 1500 m; and in numerous industrial situations. A particular form of gravity current occurs when the intruding fluid is made dense by the addition of many small heavy particles. Graphic examples of such flows were seen on the streets around the World Trade Centre after the tragic events of 11 September. This general form of motion has been extensively studied in DAMTP during the last few years.
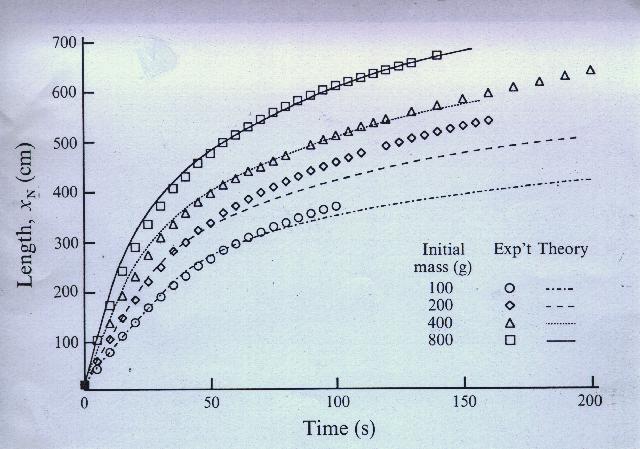
| Figure 1. The length as a function of time of particle-driven gravity currents with varying initial masses of sediment. Symbols are experimental measurements and curves are theoretical predictions for initial masses as listed. |
One of the fundamental questions to be answered is how far and at what speed a given volume of heavy, particle-laden fluid will intrude beneath a large layer of clear fluid. By numerical solution of the partial differential equations describing the motion, tested against mathematical formulae available for special, relatively simple cases, we have obtained a good quantitative understanding of the processes. The theoretical results have been carefully compared with data from laboratory experiments (fig. 1) and are in good agreement with them. Armed with these quantitative concepts we have studied large-scale natural flows such as the devastating, so-called pyroclastic flows which resulted from the volcanic eruptions on Montserrat over the last eight years (fig. 2).

| Figure 2. A recent pyroclastic flow on Montserrat. |
A typical problem posed to the theorist is: given all the initial conditions of the situation (a volcanic eruption, pollutant release, etc.), what is the final distribution of the deposit on the ground? A more difficult question, but one whose answer is needed to interpret the deposits of ancient eruptions, is: given only the final distribution of the deposit on the ground, what can be inferred about the size, intensity and duration of the event? We considered this approach in conjunction with field data collected from the eruption at Taupo, New Zealand in 197 AD. This was one of the largest explosive eruptions of the last 10,000 years and resulted in a circular deposit of about 30 cubic kilometres of solid material spread over 20,000 square kilometres, centred on the vent site. We concluded that the flow rate of solids plus gas was maintained at about 40 kilometres per second for around 15 minutes. The near-vent solids concentration in the flow was approximately 0.3% by volume and it travelled outward from the vent in a cloud about 1 kilometre thick at a typical speed of 200 metres per second.
The particulate concentration, though low, was sufficient to keep the pyroclastic flow attached to the ground. At lower concentrations, after some of the particles have been deposited, the resulting hot flow can become less dense than the surrounding, colder air and will then rise vertically, ascending many kilometres into the atmosphere. This form of subsequent motion, known as a co-ignimbrite cloud by geologists, occurred to the pyroclastic flow resulting from the Mt. St. Helens eruption in 1980 after it had propagated a distance of about 18 kilometres. A number of witnesses reported that they saw the pyroclastic flow approach them and they were prepared for the worst when it suddenly lifted off the ground. They did not know (or care?) about the scientific explanation, but were all very grateful. We have been able to calculate in detail when such behaviour will occur.
Another study we have undertaken considers the influence of a mean flow - wind in the atmosphere or current in the oceans - on the propagation of gravity currents. This investigation was conducted in response A to a request from a Government Agency who were asked to regulate a new dredging technique whereby water at high pressure is released from a long horizontal nozzle close to the harbour bed. Sand particles are lifted into the water column and are then meant to be transported out to sea by a favourable tide. How far out to sea will the sand be deposited, was the initial question put by the Agency. They were somewhat horrified to be told, and shown in an experimental demonstration, that no matter how strong the (tidal) current, some of the heavy sand would be deposited upstream of the original dredging point, that is further A into the harbour. We were able to calculate the maximum upstream penetration as a function of the magnitude of the current and size of the particles to yield results which were in excellent agreement with our laboratory simulations.
| From the Ozone Layer to Ocean Waves Professor Michael E McIntyre, Department of Applied Mathematics & Theoretical Physics (DAMTP) http://www.atm.damtp.cam.ac.uk/people/mem/ |
How can man-made chlorofluorocarbons (CFCs) emitted in the Northern Hemisphere give rise to an ozone hole in the Southern Hemisphere? The answer to this question involves a complex interplay between fluid dynamics, chemistry, and ultra-violet and infra-red radiation, as already sketched in an earlier Asymptopia article (issue No. 4, March 1999) about a spinoff in understanding the Sun. A key point is that the global-scale stratosphere acts as a huge "gyroscopic pump", with the Earth's rotation playing a central role. The pump drives a global-scale circulation that moves greenhouse gases around, taking them through stratospheric regions where hard solar ultra-violet radiation can induce chemical changes, such as the breakup of man-made CFCs and the consequent ozone depletion.
Figure 1 shows a snapshot of the pump in action, made visible by remote sensing from space. An animated version can be seen on my website
and shows the central purple region rotating clockwise through an angle of about 70 degrees during 5 days, 10-15 August 1997.
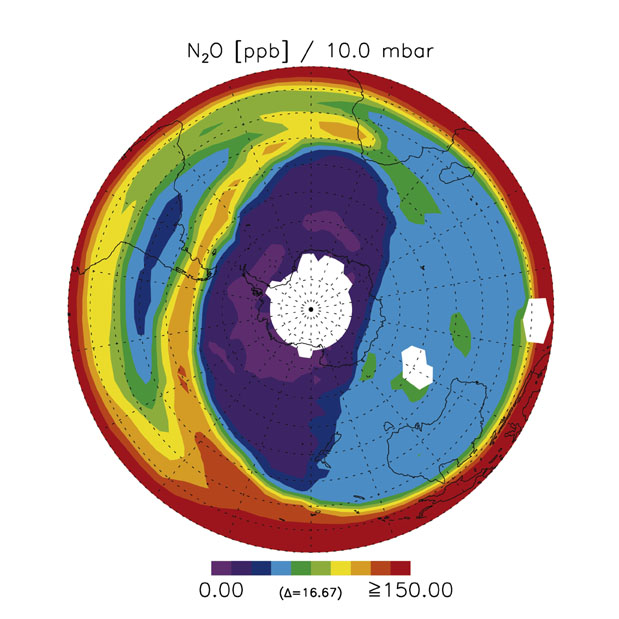
| Figure 1. Distribution, at about 30 km altitude, of a chemical tracer, nitrous oxide, which for present purposes is accurately inert. The pattern is shaped by horizontal air motion. It reveals distinct airmasses such as the well-mixed blue region on the right, sandwiched between relatively isolated polar and tropical airmasses, with steep tracer gradients in between. A long tongue of tropical air (orange-yellow) marks an early stage in a typical mixing event. Image by courtesy of my colleagues Dirk Offermann and Martin Riese of the CRISTA remote-sensing project. The whole picture involves an intimate interplay of wavelike and turbulent dynamics leading to irreversible momentum transfer and gyroscopic pumping: a highly inhomogeneous "wave-turbulence jigsaw puzzle", whose functioning - entirely outside the scope of classical turbulence theories - was first understood through mathematical modelling done in DAMTP by Professor Peter Haynes and others. |
How does the pump work? The Atmospheric Dynamics group in DAMTP is well known for its pioneering contributions to answering this question through mathematical modelling. Part of the story concerns the rotation of the central purple region. This is the so-called "polar vortex". Its long axis rotates at a rate determined by a competition between the winds - which blow clockwise, at speeds of the order of 180 miles per hour, about nine times faster than 70 degrees in 5 days - and a certain wave propagation mechanism that tries to rotate the long axis the other way. It is called the "Rossby-wave" mechanism. The evidence for inhomogeneous horizontal mixing (see figure caption) shows that the Rossby waves must be considered to be breaking. The upshot is a momentum transfer corresponding to a westward force on the stratosphere and an eastward reaction on the denser air below. The momentum transfer powers the gyroscopic pump.
A spinoff from all this is, perhaps surprisingly, a set of new ideas about how wind generates the great ocean waves that can threaten shipping. What on earth, you might ask, has the global-scale stratosphere to do with ocean waves? The answer lies in the airflow above the waves. Though superficially different-looking, it involves a fundamentally similar Rossby-wave mechanism and momentum transfer, essential for wave generation.
| CRIGHTON BENEFIT CONCERT |
Classical music lovers and admirers of David Crighton may have heard about the remarkable charity concert held in David's memory last May, organized by Johanna Crighton. The excitement and atmosphere were captured in a professionally-produced recording, now available. The 2-CD set can now be obtained at the bargain-basement price of just £10, plus £1 for postage & packing. Solve some of your Christmas-present problems, support a worthy cause, and help remember a very wonderful person who always strove to promote the public understanding of, and engagement with, science and mathematics.

Audio clips from the recording (mp3) and more information about the charities and the music are available at the website www.atm.damtp.cam.ac.uk/people/mem/crighton.html. The CDs can be obtained either from the Cambridge University Press Bookshop, 1 Trinity St., Cambridge, UK (tel 01223-333333 or +44-1223-333333, fax 332954, email bookshop@cambridge.org, payment by cash, cheque, or credit card), or from Mrs Rita Gaggs, 2 St Marks Court, Barton Road, Cambridge CB3 9LE, UK, (0)1223 565913 oliver.gaggs@geo2.poptel.org.uk, who can accept cheques in UK £ to either of two charities: "David Crighton Music Fund" if you'd prefer to support young musicians, or "University of Cambridge (David Crighton Fund)" if you'd prefer to support mathematical research.
The programme consisted of three glorious piano trios, passionately performed by three artists who knew David personally: Haydn's Trio in A major (1785), Hob. XV:9, the great Schubert in B flat major (1825-7), D 898, and the mighty Dvorak in F minor (1883), Op. 65 - plus an encore given after nearly two-and-a-half minutes of applause at the end - the deeply-felt third movement of Schumann's Maerchenerzaehlungen Op 132 - all of it great music resonating with David's life in many ways, speaking of joy in the face of adversity, of his love of his fellow humans, and of his radiant optimism for the future.
| The Future of Theoretical Physics and Cosmology: Stephen Hawking 60th Birthday Symposium Professor Gary Gibbons, Dr Stuart Rankin and Dr Paul Shellard (DAMTP) |
On Tuesday 8 January 2002, Stephen Hawking will be 60. For any world-class scientist this would be sufficient reason for marking the event with a major international conference, but in the case of Professor Hawking there are particular reasons to celebrate, not just because of his personal triumph over physical infirmity but also his unique contribution to the popularization and dissemination of fundamental ideas about physics and the universe. The conference, entitled ``The Future of Theoretical Physics and Cosmology'' will be held at the Centre for Mathematical Sciences in the University of Cambridge from 7-11 January, 2002. It will be composed first of a four-day scientific workshop, featuring specialist lectures by 43 of the most distinguished scientists in theoretical physics and cosmology.
The last day of the conference, Friday 11 January 2002, will be a one-day symposium of popular lectures for a broader audience and for which we anticipate wide media coverage. It will be held in the CMS central core and amongst the 400 participants many will be graduate students and young researchers drawn from Cambridge and other UK Universities. The programme of speakers for the symposium includes Sir Martin Rees, Sir Roger Penrose, Professor James Hartle, Professor Kip Thorne, and Professor Stephen Hawking himself. Tickets are by invitation only, but those with queries may address them to the conference secretary, Jennifer Formichelli, at:
Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 OWA.
Tel: 01223-765317, Email: J.L.Formichelli@damtp.cam.ac.uk.
The Local Organizing Committee wishes to thank the following sponsors for their generous support which has made this landmark conference possible: Physics and Astronomy Research Council (PPARC), Silicon Graphics Computer Systems, the London Mathematical Society, the University of Cambridge, the Clay Mathematics Institute, Cambridge University Press, Trinity Hall, Gonville & Caius College and Mr Dennis S Avery.
| News in Brief Patrick Hawke-Smith, Cambridge University Development Office |
Actuaries at Cambridge
The Actuaries' Room at the Centre for Mathematical Sciences is named in recognition of gifts from one hundred and twenty members of the actuarial profession. We were delighted that many were able to come to Cambridge earlier this year to view the Room and a special Book of Benefactors. We hope to build on this event to strengthen the links between the profession and Cambridge Mathematics.
Friends of Mathematics
The seventh meeting and dinner of the Friends of Mathematics at Cambridge University was held on Tuesday 16 October. Good weather allowed guests to see the Centre for Mathematical Sciences in its nigh full splendour. They then enjoyed presentations on some current mathematical activities, followed by a reception and dinner at St John's College. We are very grateful to Mr Hugh Stewart (St John's, 1947) for his support of the dinner and his enlightening talk on the history of the last wooden spoon. This fine object, on display at the dinner, was awarded to C L Holthouse for receiving the lowest mark in the mathematical tripos in 1909, the final year in which results were individually ranked.
The "Friends" event offers a pleasurable way to recognise some of the key supporters of Mathematics at Cambridge and we look forward to gathering again next year.
List of donors
Thanks go to all those who responded to the list of donors published with the September edition of Asymptopia. Apologies are due to the London Mathematical Society, whose name should have appeared in the list of donors to the David Crighton Fund. We are also pleased to acknowledge the support of Professor Sir Hermann Bondi for the David Crighton Fund and Mr T E Wood.
New donations
We are grateful to the Thriplow Trust for a donation that makes in possible for us to continue publishing Asymptopia. For information on making a donation in support of any aspect of Mathematics at Cambridge, please contact Professor Peter Landshoff
(P.V.Landshoff@damtp.cam.ac.uk) or Patrick Hawke-Smith (ph250@cam.ac.uk).
Asymptopia
Please send any corrections to the mailing details for Asymptopia to the Cambridge University Development Office at 10 Trumpington Street, Cambridge, CB2 1QA, UK (fax: +44 (0)1223 460817, email: database@foundation.cam.ac.uk).
