
|
In February 1999, Dr Dill Faulkes made an exceptionally generous donation of a million pounds to the Isaac Newton Institute for Mathematical Sciences, to construct a neighbouring building on the Clarkson Road site, to be known as the Faulkes Gatehouse. The building has been designed as part of the Centre for Mathematical Sciences (CMS) on the Clarkson Road site by the architect Edward Cullinan, and has been built, together with the neighbouring new Betty and Gordon Moore Library of Science and Technology, by Sir Robert McAlpine.
The Gatehouse provides access through an attractive archway to the main CMS site from the east (Cambridge) end of the site. It comprises office space at ground floor level, and a semi-circular seminar room at first floor level accommodating up to 50. Assigned to the Newton Institute, it will allow a valuable expansion of research activity at the Institute, and accommodation for visiting Research Fellows, including possibly those funded by Industry.
Dr Dill Faulkes has made a further magnificent donation of £2.5M to fund construction of Pavilion E on the same site, to be known as the Faulkes Institute for Geometry; this building is currently being built and will be ready at the beginning of next year.
 |
| Dr Faulkes and McAlpine works manager Len Bogic quaff ale after the topping out, in which Dr Faulkes fixed a sprig of yew to the top of the building. |
The Topping-Out Ceremony on Monday 19 February marked the completion of the construction of the Gatehouse, and gave the Vice-Chancellor an opportunity to thank Dr Faulkes for his great generosity to the University and to the Newton Institute.
Meanwhile, Laings, who were responsible for the first buildings on the site, have just begun work on the remaining three buildings, so that the whole of the 60 million pound project will be completed by the end of next year - but a small funding gap remains!
| If you are contemplating making a donation, you are most welcome to discuss it with Anthony Tootal, Acting Director of the University Development Office ajt27@cam.ac.uk, or with Professor Peter Landshoff P.V.Landshoff@damtp.cam.ac.uk. Advice for American citizens on tax-efficient giving to the University may be obtained from the Cambridge University Development Office in the United States cambrdgusa@aol.com. |
| The GK Batchelor Laboratory of Fluid Dynamics Dr S B Dalziel, Director of the Fluid Dynamics Laboratory Department of Applied Mathematics and Theoretical Physics |
"But I thought this is a maths department!" This is often the response when someone discovers DAMTP has a fluid dynamics laboratory. Since DAMTP first moved to the Press Site in 1964, mathematicians - along with a scattering of physicists and engineers visiting the Department - have got their hands wet deep in the 'wetting cellar' of the old University Press building.
For nearly forty years the Laboratory has thrived, despite a lack of adequate drainage, low ceilings, and increasingly cramped conditions. A symbiosis has developed where the interplay between experimental studies and other modelling activities have led to the experiments in DAMTP being quite different to those found in most other departments. The experiments help us to construct appropriate mathematical models, and provide the data to validate the models. The art is in designing a simple experiment capable of providing a generic question.
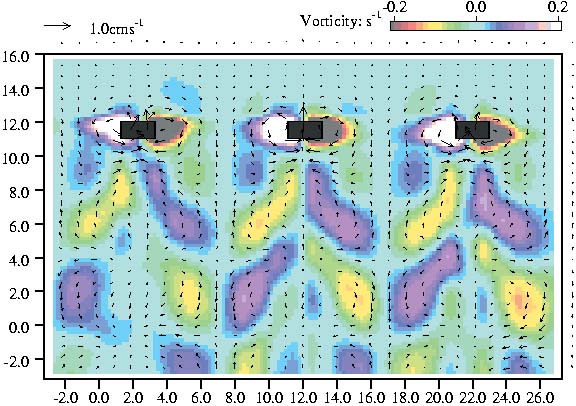 |
| Time average flow behind a grid generating turbulence in a stratified fluid. (R C Higginson and S B Dalziel) |
The Laboratory is perhaps best known for its work in geological, geophysical and environmental fluid dynamics. However, experiments spanning nearly the full spectrum of fluid dynamics have been undertaken: from swimming algae to flow through fractal objects; from breaking liquid bridges to spin-stabilised satellites; from microbubbles to crop spraying; from salt fingers to solitary waves.
Some of the questions being asked in the Laboratory are practical: how do topography and salinity interact with tidal currents to control the dispersion of pollution from bays, and how is this process related to the flushing of pollutants from our city streets? What governs the crystallisation of magma, or the progress of a pyroclastic flow from a volcanic eruption? What is the effect of wind conditions on buoyancy driven ventilation in a building, and how can we use this to our advantage? Can we control the hydrodynamic instabilities that limit the efficiency of inertially confined fusion? Other questions are more fundamental, but their answers invariably have practical implications: what is the best way to model granular materials? Do we understand the differences between density due to heat or composition from that due to the presence of a suspended second phase? Is mixing sensitive to how we put the energy into the system? How do fluids accommodate mathematical singularities?
When it was founded, the concept of a laboratory in a mathematics department was unique. Since then, many leading mathematics departments have witnessed the success of the Laboratory and have set up one of their own, although none have had the scale or scope of that in DAMTP. With the new facilities at CMS the Laboratory may still be hidden underground, but we anticipate that it will become even more visible to the research community!
| The GK Batchelor Fund We invite you to help establish a fund in the memory of George Batchelor to support experimental work in fluid mechanics. |
DAMTP in particular owes a lot to Batchelor: he was instrumental in the founding of the Department in 1959, and remained Head of Department from then until his retirement in 1983. Batchelor was also responsible for establishing the Laboratory. He foresaw an immense benefit to the fluid dynamics community in having the leading theoreticians undertaking (or at least being closely involved with) experiments designed for probing the basic elements of fluid dynamics.
In recognition of his pivotal role in fluid mechanics and in establishing the Laboratory, it has been agreed that the new Laboratory at CMS will be named the GK Batchelor Laboratory of Fluid Dynamics.
We now seek to establish an endowment fund, the GK Batchelor Fund, which will be used to provide vital support new experimental initiatives within the Laboratory. We believe that Batchelor would have seen this proposal as particularly appropriate. Your support will help ensure continuation of the great tradition of research in fluid dynamics in which Batchelor provided such inspiring leadership.
| The world of fluid mechanics will have been greatly saddened by the death of Professor George Keith Batchelor FRS on 30 March 2000. Batchelor will be remembered for many outstanding achievements: in his own fluid mechanics research, for his textbook An Introduction to Fluid Dynamics, the establishment of the European Mechanics Committee and EUROMECH Colloquia, and the founding of (and his forty years editing) the Journal of Fluid Mechanics. |
|
| UK and other non-US donors - if you would like to support the GK Batchelor Fund, please contact: Patrick Hawke-Smith, Cambridge University Development Office, 10 Trumpington Street Cambridge CB2 1QA, UK. ph250@foundation.cam.ac.uk UK income tax / capital gains tax payers - please note that your donation can be made under the Gift Aid scheme, increasing its value by 28% at no additional cost to you. US donors - please send your donation, made payable to CUDOUS, to The Cambridge University Development Office in the United States (a section 501(c)(3) organisation) at: CUDOUS, 708 Third Avenue, 14th Floor, New York, NY 10017, USA. |
| Cosmology: singular science Professor Neil Turok, Department of Applied Mathematics and Theoretical Physics |
Is cosmology a science? By traditional criteria the answer would surely be "no". There is only one Universe, and even if we think of that as the result of a giant experiment, it is an experiment that cannot be repeated. Indeed cosmology seems more like science fiction when it ventures to discuss the beginning of the Universe, and the causes of the hot big bang. As a quantitative subject, cosmology has until recently been relatively weak, with most of the information deriving from observations of remote and inaccessible objects. The observations are almost always very difficult and fraught with possible artefacts.
In spite of these difficulties and uncertainties, cosmology is set to play an increasingly central role in science in the years ahead. In part this is due to the tremendous advances in observations. Almost all the theoretical models which were around just 10 years ago have been convincingly ruled out, and discrepancies of 10% between theory and observation are now taken seriously. The next decade promises still greater precision. But science is more than data, and the second reason for cosmology's advance is that theory is doing surprisingly well. General Relativity is the foundation of cosmology, but additions such as cosmic inflation are allowing us to make and test predictions on questions where General Relativity provides no answer, such as the origin of structure.
 |
 |
According to the most recent data, the Universe is roughly 70% cosmological constant (or vacuum energy), 25% dark matter, 5% ordinary matter (atoms, nuclei and electrons), something above a third of a per cent massive neutrinos, and one part in ten thousand radiation. It seems an arbitrary mix, which we do not understand. But this composition fits data from galaxy formation and clustering to the abundance of the light elements and the relic cosmic microwave sky, a remarkable 'concordance'. Work now focuses on 'cracks' in the concordance model, where inconsistencies are emerging as the data and theoretical calculations improve. Whilst cold dark matter reproduces the observed clustering on large scales, it over-produces small galaxies and does not predict the voids seen in the galaxy distribution. Alternatives including 'warm' dark matter do better. Improved tests and data will give powerful clues as to the nature of the dark matter.
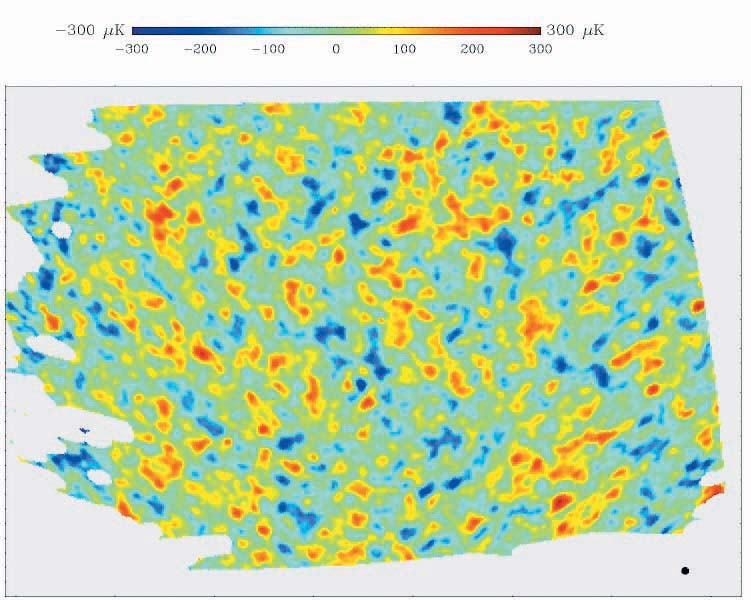
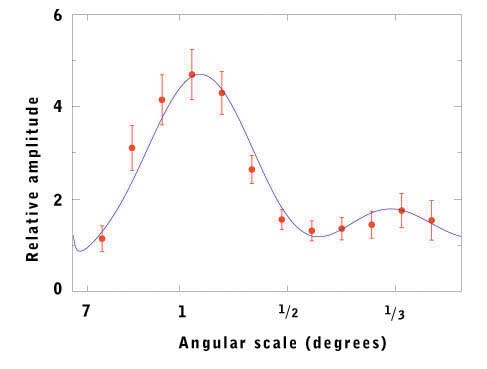
A dramatic advance last year was the first detailed mapping of the cosmic microwave sky. The relic microwave radiation gives us a view of the universe only three hundred thousand years after the big bang. The Boomerang collaboration, flying a balloon-born telescope around the south pole, mapped a 20 degree square patch of the sky, revealing variations of a few parts in a hundred thousand, originating in the early Universe. These density variations first grow and then oscillate as time advances. The oscillations lead to a series of peaks peak in the fluctuation level on angular scales below a degree or so. The discovery of the first peak by Boomerang and other experiments has transformed the debate on the physical origin of the fluctuations, lending support to simple models of inflation. The scale of the peak in power (see graph) also indicates that the universe is close to being spatially flat. A theory of the origin of these fluctuations, linking quantum mechanics to gravitation, was developed in the early 1980's following the invention of inflation. During an inflating epoch preceding the hot big bang, minute quantum mechanical 'vacuum' fluctuations are stretched and amplified into large scale structure similar to what we see today. The apparent flatness of the universe is also a success for the idea of inflation.
So far there is no deep foundation for models of inflation, which tend to resemble 'Heath-Robinson' constructions. Nevertheless the calculations provide an intriguing glimpse of an observational consequence of quantum gravity, the holy grail of theoretical physics. If this explanation is correct, quantum mechanics was actually central to the origin of galaxies, stars and planets!
The progress in cosmology has not so far been connected with fundamental theories of quantum gravity based on supergravity and superstrings. It is hoped the developments will merge, and a theory consistent with both reality and mathematics will result. But for the moment things are not working out that way. There is now evidence for a positive cosmological constant. But according to supergravity, there are no classical solutions with positive cosmological constant, and therefore no candidate for the future state of the Universe. Likewise inflation relies on a temporary cosmological constant to drive the expansion of the early Universe. But this also seems inconsistent with supergravity.
Over the next few years we can look forward to a plethora of new data. This June NASA will launch the MAP satellite which will picture the cosmic sky at a resolution of a third of a degree, and in 2007 ESA's Planck satellite will do so with a resolution of a tenth of a degree. There will be an intense effort in Cambridge and elsewhere to compare theories with data. Many other measurements, including large scale and high redshift galaxy surveys, gravitational wave detectors, and X ray satellites, will help complete the picture. Of course the real challenge will be to fit these observations into a consistent theory, the development of which will be one of the great challenges of the next decade.
| Diffusion, Finance, and Universality Professor Geoffrey Grimmett, Statistical Laboratory |
Seen from a distance, the water in a beaker appears to be motionless, but this is an illusion. Aided by sufficient magnification, one would see that each molecule of water enjoys a motion which is unceasing and without apparent order.
The exact history of this observation is murky. A revolutionary microscope design enabled Antony van Leeuwenhoek (1632-1723) to observe the apparently random motion of micro-organisms, which he dubbed "animalcules". Such motion is biological in cause. Credit for noticing that all sufficiently tiny particles - animal, vegetable, mineral - will enjoy a disordered movement of physical origin is usually given to the Scottish botanist Robert Brown (1773-1858). Brown's 1827 observations began with particles contained in pollen grains suspended in water, followed soon by "every mineral which I could reduce to a powder", including arsenic and "a fragment of the Sphinx". In every case, his "active" particles showed a ceaseless and erratic movement, later termed Brownian motion.
 |
| Brown's microscope, in the possession of the Linnean Society. Courtesy of Brian J Ford, whose advice on the history is acknowledged. |
Brown could hardly have anticipated the fact that Brownian motion now occupies a central position in mathematics and its applications. Viewed as a mathematical subject, it has extraordinary intrinsic beauty, and is pivotal for many models in areas as widely spread as physics, finance, and statistics. Brownian motion is implicated in most situations involving the aggregate of a large number of random effects, and an evolution in time.
The experimentalists were followed by the theoretical physicists, and then the mathematicians. A physical theory of Brownian motion was advanced by Einstein in 1905. He established amongst other things a formula for the rate of diffusion in terms of physical constants, a result which enabled Perrin to calculate Avogadro's number from Brownian experiments, and which aided Perrin's Nobel prize in 1926. The major defect in Einstein's theory lay in the problem of defining the velocity of a diffusing particle.
Brownian motion is at the heart of modern probability theory. It is the keystone of the theory of diffusion, and it arises naturally in a multitude of other settings. A major thrust of the last fifty years has been to understand how to solve differential equations containing terms which are random. For example, a general diffusion equation takes the form dX = m dt + s dB, where m is the drift of the process X, s is a volatility, and B is a Brownian motion. Just what is meant by such a stochastic differential equation, and how one may study its solution, fall within the modern domain of stochastic calculus, an area which combines the tendency of pure mathematicians towards deep abstraction with the driving need of applied mathematicians and engineers to describe the behaviour of practical systems.
A Nobel prize of greater contemporary note than Perrin's was that awarded in 1997 to Scholes and Merton for their mathematics of finance. The idea of using Brownian motion in a financial model may be found in the 1900 thesis of Louis Bachelier entitled Théorie de la Spéculation. Bachelier's work was discounted at the time, but has attracted a great deal of attention since. A more satisfactory model than Bachelier's is 'geometric Brownian motion' - the logarithm of the market price, rather than the price itself, follows a Brownian motion - and this is the modelling assumption made by Black and Scholes in their no-arbitrage computation of the value of a European call option. Finance is now a major application of mathematics. Although the associated mathematics is rich and beautiful, it has proved an error to adhere over rigidly to strategies based on mathematical facts.
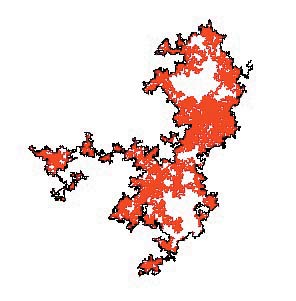 |
| The frontier of two-dimensional Brownian motion. Courtesy of Oded Schramm. |
We turn now to current research. Astonishing progress has been made in recent months on the physical question of 'universality' in two dimensions. In brief, physicists have made remarkable predictions concerning exact calculations involving phase transitions, and it has been a mathematical challenge of the first order to verify these. Recent mathematical progress threatens to lift the veil in two dimensions, where special methods related to so-called 'conformality' are valid. Only one peripheral illustration is included here, namely the problem of the frontier of two-dimensional Brownian motion. Suppose, as in the figure, we run a Brownian motion up to some fixed time. We see a shape, containing holes, whose frontier is rough. Indeed, the frontier is so jagged that it is not really a simple line, but has a dimension lying between one and two. It has been a famous conjecture of Benoit Mandelbrot that the dimension of the frontier is 4/3. This has been proved recently, as part of an extensive programme which promises to explain a panoply of mysterious (for mathematicians) predictions about physical models in the plane.

