Contents
The final three pavilions were completed just before Christmas and the remaining half of the Department of Applied Mathematics and Theoretical Physics has now moved to the site. The department is pleased to be reunited after three years of split-site working. It joins the Department of Pure Mathematics and Mathematical Statistics; the two departments are pleased to share a site for the first time and look forward to the closer relations that this will make possible.
Congratulations to Anne Davis, who is the first woman in the Faculty to become a professor. Her research subject is particle physics and cosmology. Congratulations also to Mrs Toni Beardon, who has been honoured by the Queen with an OBE for her work on NRICH. NRICH is a part of the Millennium Mathematics Project, a collaboration between Mathematics and Education to show children that mathematics is interesting, important and not all that difficult. See www.nrich.maths.org.
Our appeal for funds in memory of David Crighton has raised nearly £200,000. This has enabled us to advertise four fellowships for research students or young postdoctoral researchers to work in fluid dynamics, David's subject.
 |
| Spring flowers on the roof of the CMS Central Core |
Back to top of page
The history of computer technology has involved a sequence of changes from one type of physical realisation to another - from gears to relays to valves to transistors to integrated circuits and so on. Today's advanced lithographic techniques can create chips with features only a fraction of a micron wide. Soon they will yield even smaller parts, and inevitably a point will be reached where logic gates are so small that they are made out of only a handful of atoms.
On the atomic scale, matter obeys the rules of quantum mechanics, which are quite different from the classical rules that determine the properties of conventional logic gates. So if computers are to become smaller in the future, new, quantum technology must replace or supplement what we have now. However, quantum technology can offer much more than cramming more and more bits to silicon and multiplying the clock-speed of processors: it can support entirely new kinds of computation.
To explain what makes quantum computers so different from their classical counterparts, let us have a closer look at a basic chunk of information, namely one bit. A bit is a physical system which can be prepared in one of two different states representing logical values - no or yes, false or true, or simply 0 or 1.
For example, in today's digital computers, the voltage between the plates in a capacitor represents a bit of information: a charged capacitor denotes bit value 1 and an uncharged capacitor bit value 0. One bit of information can also be encoded using the two different electronic states of an atom. However, if we choose an atom as a physical bit then quantum mechanics tells us that apart from the two distinct electronic states, the atom can be also prepared in a coherent superposition .of the two states. This means that the atom is both in state 0 and state 1. There is no equivalent of this superposition in the classical physics we encounter in the every day world, and such quantum phenomena often seem counter-intuitive.
Let us push the idea of superpositions of numbers a little further. Consider a register composed of three physical bits. A classical 3-bit register can store exactly one of eight different numbers in one of the eight possible configurations 000, 001, 010, ..., 111, representing the numbers 0 to 7. But a quantum register composed of three quantum bits, or qubits, can simultaneously store up to eight numbers in a quantum superposition. If we add more qubits to the register its capacity for storing quantum information increases exponentially. A 250-qubit register - essentially made of 250 atoms - would be capable of holding more numbers simultaneously than there are atoms in the known universe. Once the register is prepared in a superposition of many different numbers, we can perform mathematical operations on all of them at once. In this way a quantum computer offers an enormous gain in the use of computational resources such as time and memory.
Several of the superior features of quantum computers have applications in cryptography. One of them is the quantum algorithm discovered in 1994 by Peter Shor of AT&T's Bell Laboratories in New Jersey, for factorising large integers efficiently. The intractability of factorisation underpins the security of what are currently the most trusted methods of encryption, in particular of the RSA (Rivest, Shamir and Adelman) system, which is often used to protect electronic bank accounts. Once a quantum factorisation engine (a special-purpose quantum computer for factorising large numbers) is built, all such cryptographic systems will become insecure: any RSA- encrypted message will become readable moments after the first quantum factorisation engine is switched on.
Admittedly, that day is probably decades away. A more simple type of quantum computation - now routinely carried out in the laboratory and likely to be a commercial proposition soon - is quantum cryptography. It is already feasible because it requires only one qubit and one quantum computational step at a time. It provides perfect security since, unlike all classical cryptography, it relies on the laws of physics rather than on ensuring that successful eavesdropping would require excessive computational effort.
In principle we know how to build a quantum computer: we start with simple quantum logic gates and connect them up into quantum networks. A quantum logic gate, like a classical gate, is a very simple computing device that performs one elementary quantum operation, usually on two qubits, in a given time. Of course, quantum logic gates differ from their classical counterparts in that they can create, and perform operations, on quantum superpositions. Simple quantum logic gates involving two qubits are being realised in laboratories both in U.K. and abroad. The next decade should bring control over several qubits and, without any doubt, we shall begin to benefit from our new way of harnessing nature.
Our newly-established Centre for Quantum Computation has several web pages and links devoted to quantum computation and cryptography (see http://cam.qubit.org).
Back to top of page
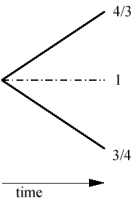
Mathematicians who work in the finance industry use simple mathematical models to help them price and hedge various deals. Let's take a look at a very simple but widely-used model for the movement of a share price, and see how it can help with this.
| The model has just two assets, a share and cash. Both are worth 1 at the start of the trading day and at the end of the trading day cash is worth 1, whereas the value of the share is 4/3 if the day was good, 3/4 if the day was bad. Investors have to pick their holdings of the two assets at the start of the day, and do not change their holdings during the day. The figure represents this situation: |
 |
|
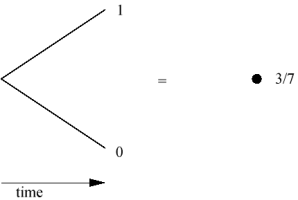
In this simple model, if a bank had made a deal which obliged them to pay 1 at the end of a good day, and 0 at the end of a bad day, then they could exactly replicate this payout as follows: at the start of the day, the bank invests 12/7 in the shares, and -9/7 in cash (that is, borrows 9/7). At the end of a good day the value of the 12/7 shares would be (4/3) x (12/7) = 16/7; paying off the debt of 9/7 would leave exactly 1. On the other hand, if the day was bad, the shares would be worth (3/4) x (12/7) = 9/7 at the end of the day, and this would be just enough to pay off the debt of 9/7. The situation is represented schematically to the right:
|
 |
|
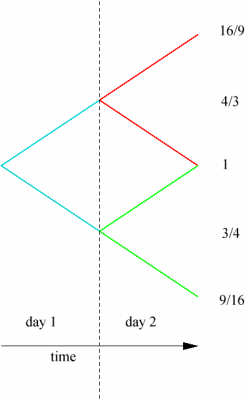
Now we can consider a two-day model along the previous lines; in the second day, the value of cash remains constant, but the value of the share either gets multiplied by 4/3 or by 3/4, so at the end of the second day the share is worth 16/9, 1 or 9/16, as in the figure to the right:
We can again replicate any payout at the end of the second day by firstly applying the above argument to reduce (or, more colourfully, `prune') the red branches of the tree to a single point value, then prune the green branches to a single point value, and finally to apply the single-day argument to compute the value at the start of day 1. The figure below illustrates this schematically:
|
 |
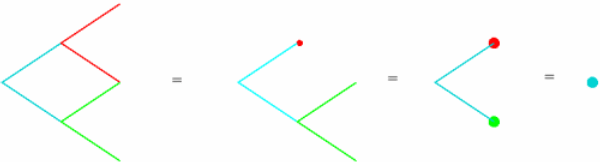
Of course, this procedure can be extended to a general model for any number of days, by successively pruning away time layers in the tree. Deals whose value at the final time depend only on the value of the share at that time (so-called European options) are easily dealt with by this method. However, there are more complicated but very important options which are beyond its reach.
What methods can then be used? The `fail-safe' method is simulation; simply use a computer to simulate many thousands of paths of the random processes, compute the value of the deal on each path and average. This will typically give much poorer accuracy than other methods, but is easy to code, and is extremely robust. Does it always work? No: we can see why not in the example of a so-called American put option, which allows the holder to sell a share for a fixed price at any time of his choosing before the end of the year. For such an option, the simulation method hits problems, because we do not know when the holder should choose to sell. Such options are widespread in practice, but are very difficult to price and hedge, especially when the amount the holder receives depends on the values of many underlying assets, as it may. Methods developed through the 90s allowed remarkably good lower bounds to be computed for the prices; only in the last three years have methods been developed to compute upper bounds, which turn out usually to be usably close to the lower bounds, thus providing a universal approach to these important practical problems. The method leading to these upper bounds is a simple application of some deep, abstract mathematics from the general theory of stochastic processes.
We can expect to see many other examples of mathematical discoveries pursued initially for their own sake turning out to be of real practical importance. Who can tell whether hard results on interacting particle systems may not turn out to be exactly what is needed to understand the interactions of agents in a market? Certainly the really challenging problems in finance now are ones which depend in some way on interactions, and future research will focus on these issues.
Back to top of page
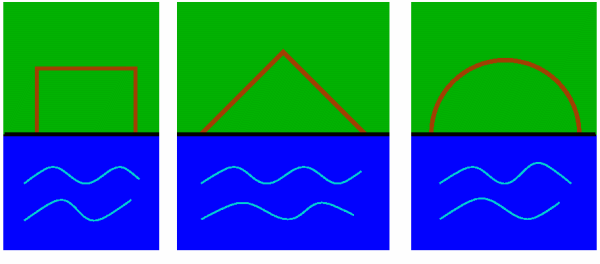
When Dido learnt that her brother Pygmalion, king of Tyre, had slain her husband Sychaeus, she set sail from Tyre, and eventually arrived on the coast of Africa. She purchased from a local chieftain, Iarbas, `as much land as she could enclose within a bull's hide'. Her followers cut the hide into thin strips, and tied them together, creating one long strip. They then placed this strip so that, together with the coastline, it enclosed a large area of land. On this land Carthage was built.
Cutting up the bull's hide to form one long, thin strip was certainly a very clever idea. However, once the strip had been made, Dido (had she been a mathematician) might have sought to arrange it in such a way that, with the straight coastline, it enclosed the greatest possible area. What shape should she have chosen? Should the strip have been in the form of three sides of a square (with the coastline forming the fourth side), or two sides of a triangle, or a semicircle, or perhaps some other shape?
Dido's problem is an example of an isoperimetric problem. We are asked to find, among all shapes of a given perimeter length, the one of maximum area. Of course, we must specify exactly what we mean by the perimeter. Here, for example, the length of coastline involved is irrelevant: it is the boundary of the shape off the coastline that must have length equal to the length of the strip of hide.
Let us suppose that the strip of hide is 600 metres long, and calculate the areas of some of the possible shapes. If the shape enclosed is a square, then each side of the square is 200 metres, so the area is 40,000 square metres. If it is an equilateral triangle, then each side has length 300 metres, and this gives an area enclosed of about 39,000 square metres. If the strip is in the shape of a semicircle, however, then it encloses an area of about 57,000 square metres. In fact, a semicircle encloses a greater area than any other shape, and so Dido should have laid her strip of hide in the form of a semicircle.
What if Dido had wished to purchase some land away from the coast? She would then have had to surround her land entirely with the strip of hide. This is a different isoperimetric problem. Here it turns out that a circle is the best shape. As with the semicircle in the original example, this is fairly plausible: a circle is a very smooth, very regular shape, with no bias towards any particular direction. The fact that the circle is best is known as the isoperimetric inequality in the plane. Various names are associated with this result, including the great Leonhard Euler in the 18th century and Steiner in the middle of the 19th century, but it was only at the start of this century that Minkowski was able to give a completely rigorous proof of it.
The problem of maximising the area of a shape, keeping its perimeter length fixed, is the same as that of minimising the perimeter length of a shape, keeping its area fixed. In this equivalent formulation, isoperimetric problems occur throughout nature. For example, consider a soap bubble floating through the air. Once it has formed, the bubble encloses a fixed volume of air, and surface tension forces it to try to minimise its surface area. The fact that soap bubbles are spherical indicates that, among shapes of given volume, the sphere has least surface area.
One isoperimetric inequality which is very important in mathematics is the isoperimetric inequality on the sphere. Here we are concerned with regions drawn on the surface of a sphere: this corresponds to the case where Dido is inland and is choosing an area of land so large that the curvature of the Earth becomes significant. Among regions of a given surface area, the one with the shortest perimeter is a cap - the region enclosed by a circle drawn on the sphere. A similar result holds for spheres of any number of dimensions, and this fact has many applications in analysis. Many other isoperimetric inequalities are important in areas as diverse as the study of the layout of computer chips, the design of telephone networks and the diffusion of heat.
The proofs of isoperimetric inequalities, although hard to find, can be very beautiful. As an example, suppose that we know the isoperimetric inequality in the plane, and wish to solve Dido's original problem. There is an elegant `reflection' argument, that goes as follows. Suppose we have a shape, and a semicicle, of the same length (not counting the coastline, of course). We wish to show that the area enclosed by the shape is no greater that the area enclosed by the semicircle. So consider what happens if we reflect each shape in the coastline. We exactly double each enclosed area, and exactly double the length of the curves. But the semicircle has now become a circle, and we know that, if a shape has the same perimeter length as a circle then its enclosed area is no greater than that of the circle. This shows that the original shape enclosed an area no larger than that enclosed by the semicircle.
Back to top of page